|
Opgave
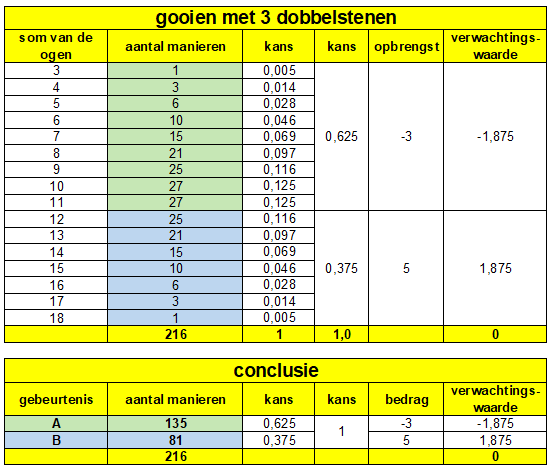
Uitwerkingen Je kunt onderscheid maken van twee gebeurtenissen A en B met:
Als het een eerlijk spel zou zijn dan zou de verwachtingswaarde van de winst (A) gelijk moeten zijn aan de verwachtingswaarde van het verlies (B). Er geldt: P(A) × 5 = P(B) × 3
Conclusie? Het is een eerlijk spel is. Er is geen speld tussen te krijgen... Toelichting In WisFaq kwam ik een vraag tegen over het gooien met drie dobbelstenen. Ik was op zoek naar een 'handige manier' om uit te rekenen wat de kans is dat je met drie dobbelsten meer dan 11 gooit. Dat lijkt lastiger dan het is. Er zijn in totaal 16 verschillende uitkomsten als je kijkt naar de som van de ogen een worp met drie dobbelstenen. De gevraagde kans verdeelt die verschillende 'sommen' in twee gebeurtenissen A en B.
De vraag is dan: wat is P(A) en P(B)? Je weet al dat de kans om 3 t/m 10 te gooien gelijk is aan een \(\eqalign{\frac{1}{2}}\). Daar komt dan de kans om 11 te gooien bij. Wat is P(11)? Er zijn 216 mogelijke manieren om met 3 dobbelstenen te gooien. Bij hoeveel manieren is de som van de ogen gelijk aan 11?
Dat zijn 27 manieren om 11 te gooien. De kans P(11)=$\eqalign{\frac{27}{216}=\frac{1}{8}}$ Conclusie: P(A)=$\eqalign{\frac{1}{2}+\frac{1}{8}=\frac{5}{8}}$ en P(B)=$\eqalign{\frac{3}{8}}$ Begrip en inzicht Als de verwachtingswaarde van het te winnen bedrag hetzelfde is als de inzet heb je te maken met een eerlijk spel of anders geformuleerd: als de winstverwachting precies nul is, dan heb je te maken met een eerlijk spel... De kunst van de uitbater is om een spel te nemen dat net niet eerlijk is. Met een negatieve winstverwachting. Denk aan roulette bijvoorbeeld.
|