|
Voorbeeld 1 "Een tentamen bestaat uit twintig 4-keuzevragen. Wat is de kans dat je meer dan de helft van de vragen goed beantwoordt als je onvoorbereid het tentamen maakt." Deze vraag suggereert dat als je een tentamen niet voorbereid je alle vragen moet gokken. Dat is natuurlijk onzin. Je kunt beter schrijven 'als je de antwoorden willekeurig invult' of iets van die strekking. Voorbeeld 2 "Op een boekenplank staat 32 boeken. Hoeveel verschillende mogelijkheden zijn er?" Dat is te vaag. Mogelijkheden? Voor wat? Zelfs als je je beperkt tot de verschillende mogelijkheden waarmee je 32 boeken op een boekplank kan zetten is het niet te doen. Er zal wel bedoeld zijn om de boeken netjes op een rijtje te zetten. Maar dat staat er niet. Voorbeeld 3 "In een vaas zitten 12 blauwe balletjes en 24 rode balletjes. Je pakt er 3 balletjes uit. Hoeveel verschillende mogelijkheden zijn er om 3 balletjes uit de vaas te halen?" Dat is ook te vaag. Mogelijkheden? Hoe bedoel je? Met de hand of met een schepje? Zelfs als je je beperkt tot de bedoelde handeling is niet duidelijk of het nu met of zonder terugleggen is. Dus helemaal fout. Voorbeeld 4 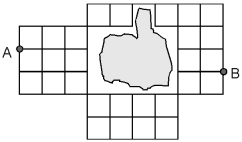
"Hiernaast staat een roosterdiagram. Hoeveel verschillende routes zijn er van A naar B?" Er zijn oneindig veel routes van A naar B. Als je dat niet bedoelt zul je iets moeten toevoegen als 'kortste routes'. In dat geval is het wel weer een aardige opgave. Voorbeeld 5 "Ik gooi met twee dobbelstenen. Bereken op 3 decimalen de kans om 5 te gooien." Dit kan verwarrend zijn. Bedoel je met '5' het totaal aantal ogen of (minstens) één dobbelsteen met 5 ogen? Dat is niet duidelijk. Voorbeeld 6 "Ik maak een toets van 20 vierkeuzevragen. Ik weet op 10 vragen het antwoord, maar moet bij de andere vragen gokken. Wat is de kans op een voldoende?" Een voldoende? Het is niet eenduidig bepaald wanneer je een voldoende hebt. Er zijn natuurlijk wel manieren voor om dat vast te stellen, maar uit de opgave wordt dat niet duidelijk. 't Is ook niet de kennis die je hier wilt toetsen denk ik. Voorbeeld 7 "Van de gebeurtenissen A en B is bekend dat P(A)=0,5 en P(B)=0,8 en P(A en B)=0,4. Kan je met deze gegevens bepalen of de gebeurtenissen A en B onafhankelijk zijn?" Als je vraagt of iemand iets kan zijn alle antwoorden goed. Een antwoord als 'nee' kan je niet fout rekenen, want de leerling heeft mogelijk naar eer en geweten eerlijk geantwoord.
|