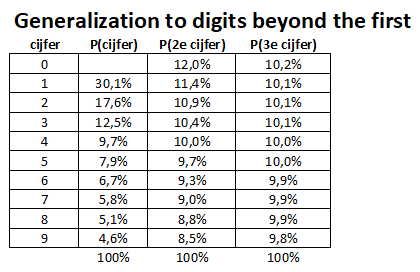
Volgens Wikipedia geldt (in het algemeen) dat de kans op het cijfer $d$ op de $n$-de plaats:

$
\eqalign{P(d,n) = \sum\limits_{k = 10^{n - 2} }^{10^{n - 1}  - 1} {\log \left( {1 + \frac{1}
{{10k + d}}} \right)}}
$

Dat geeft dan bijvoorbeeld:

In Excel heb ik de volgende functie gedefinieerd:

Function Benford(d, n)
   Start = 10 ^ (n - 2)
   Eind = 10 ^ (n - 1) - 1
   Som = 0
   For k = Start To Eind
      Som = Som + Log(1 + 1 / (10 * k + d)) / Log(10)
   Next
   Benford = Som
End Function