|
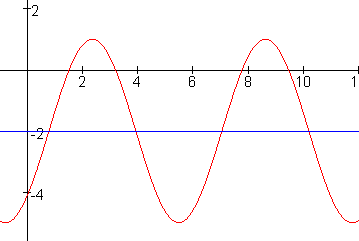
Geef aan hoe de grafieken van de volgende functies uit een standaardgrafiek ontstaan en geef de evenwichtsstand, de amplitude, de periode en de coördinaten van het beginpunt. $f(x)=-2+3\sin(x-{\textstyle{1 \over 4}}{\rm{\pi }})$
Uitwerking
$y = \sin (x)$ De evenwichtsstand is $-2$, de amplitude is $3$, de periode is $2\pi$ en de coördinaten van het beginpunt zijn $(\frac{1}{4}\pi,-2)$.
|