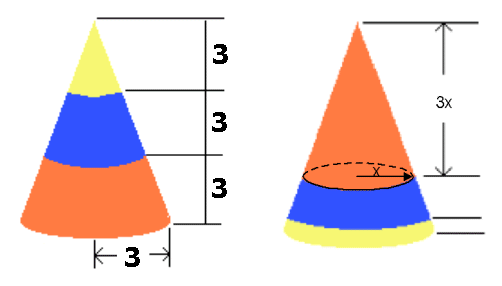
Bereken eerst de inhoud van het 'rode gedeelte' aan de linkerkant:

$
\frac{1}{3} \cdot \pi  \cdot 3^2  \cdot 9 - \frac{1}{3} \cdot \pi  \cdot 2^2  \cdot 6 = 19\pi
$

Voor het rode stuk aan de rechterkant geldt:

$
Inhoud = \frac{1}{3}\pi x^2  \cdot 3x
$

Er geldt:

$
\begin{array}{l}
 \frac{1}{3}\pi x^2  \cdot 3x = 19\pi  \\
 x^3  = 19 \\
 x = \sqrt[3]{{19}} \\
 \end{array}
$
De hoogte van het rode stuk is $
3\sqrt[3]{{19}}
$.