Machtsformules

Een machtsformule heeft de vorm $y=ax^{n}$.

In de praktijk is $n$ vaak een decimaal getal. In dat geval beperk je je tot positieve $x$-waarden.

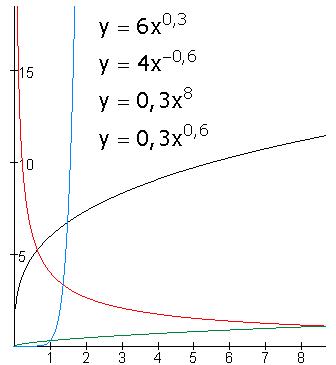
y is evenredig met een macht van x

$y$ is evenredig met een macht van $x$ betekent dat er een getal $a$ bestaat zodat $y=ax^{n}$.

Het getal $a$ heet de evenredigheidsconstante.

Voorbeeld

Is $y$ evenredig met $x^{2,3}$ en hoort bij $x=3$ de $y$-waarde 8 dan geldt:

$
\begin{array}{l}
 8 = a \cdot 3^{2,3}  \Rightarrow a = \frac{8}{{3^{2,3} }} \approx 0,639 \\
 Formule:y = 0,639x^{2,3}  \\
 \end{array}
$

y is omgekeerd evenredig met een macht van x

$y$ is omgekeerd evenredig met een macht van $x$ betekent dat er een getal $a$ bestaat zodat $y=\large\frac{a}{x^{n}}$

Voorbeeld

Als $y$ omgekeerd evenredig is met $x^{2}$ en voor x=6 is y=12 geef dan de formule.

$
\begin{array}{l}
 y = \frac{a}{{x^2 }} \Rightarrow 12 = \frac{a}{{36}} \Rightarrow a = 432 \\
 Formule:y = \frac{{432}}{{x^2 }} \\
 \end{array}
$

Aantonen dat uit een tabel volgt dat y evenredig is met xⁿ

Bereken bij elk onderzoeksresultaat het quotiënt $\large\frac{y}{x^{n}}$ en laat zien dat deze quotiënten gelijk zijn. Dat is dan meteen de evenredigheidsconstante $a$.

Formule: $y=ax^{n}$