|
lineaire formules
|
Bij de algemene formule voor een lineair verband tussen x en y hoort een formule van de vorm:
De grafiek van y=ax+b is een lijn die:
- 1 naar rechts en a omhoog gaat
- de y-as snijdt in het punt (0,b)
De waarde van a noemen we richtingcoŽfficiŽnt. |
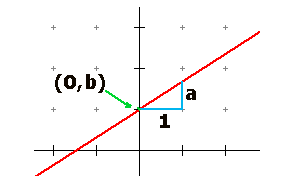 |
een parabool tekenen [1]
|
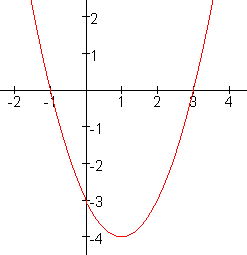 De grafiek van y=x2-2x-3 De grafiek van y=x2-2x-3
- Vul in: x=0. Dat geeft y=-3, dus (0,-3) is het snijpunt met de y=as.
- Vanwege de symmetrie is er nog een punt met y=-3.
- x2-2x-3=-3
x2-2x=0
x(x-2)=0
x=0 of x-2=0
x=0 of x=2
De oplossing x=0 hadden we al maar (2,-3) is dus ook een punt van de grafiek.
- Vanwege de symmetrie ligt de top bij x=1. Invullen geeft y=12-2∑1-3=-4. De top is (1,-4).
- Neem nog een paar punten (x=-1 en x=3 bijvoorbeeld) om de grafiek te tekenen
Dit werkt altijd. Behalve als de top van de parabool op de y-as ligt. Maar dat is dan niet erg want dan weet je ook meteen hoe 't zit. Hoe kom je er achter dat de top op de y-as ligt? |
[1] Dit wijkt af van de methode in het boek maar dit is wel handig...
|