|
Voorbeeld
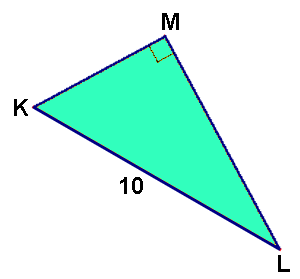
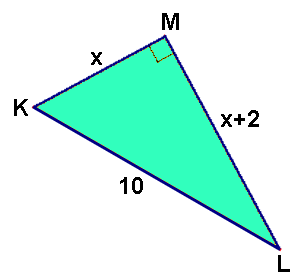
't Is een rechthoekige driehoek, de schuine zijde is 10 en de andere twee zijden weet je niet. Maar je weet wel $ML$ is 2 langer dan $KM$. Het heeft te maken met de de stelling van Pythagoras. Maar dan moet je wel minstens 2 zijden weten. Als je $KM$ zou weten zou je dan weten hoe lang $ML$ Is? Ja... Dingen als 'als ik $KM$ weet dan weet ik $LM$ ook' kunnen je op het idee brengen om voor $KM$ maar 's $x$ te nemen. Als $KM=x$, dan is $LM=x+2$. Met de stelling van Pythagoras kan je dan misschien $x$ wel uitrekenen!
De oplossing $x=-8$ voldoent niet, maar $x=6$ zou een oplossing kunnen zijn. $KM=6$ en $LM=8$, de oppervlakte van $
$
Controle: de opdracht was om de oppervlakte van $
|