• Bereken de kans op 2 witte ballen. 

Uitwerking 1

Maak gebruik van:

Aantal gunstige uitkomsten is $3·8·7·6=1008$
Aantal mogelijke uitkomsten is $14·13·12=2184$
P(2 witte ballen)=$\eqalign{\frac{1008}{2184}=\frac{6}{13}}$

Uitwerking 2

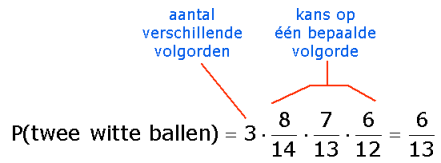
Er zijn eigenlijk twee soorten ballen: witte en niet-witte. Wat is nu de kans op (precies) twee witte ballen? Er zijn nu verschillende mogelijkheden: de eerste 2 ballen kunnen wit zijn en de derde niet, de eerste en de derde kunnen wit zijn, enzovoort....
Om de kans uit te rekenen kun je kijken naar één zo'n volgorde. We nemen maar wit, wit, niet-wit. We kijken naar P(w,w,n), dus de kans op precies die volgorde.

P(w,w,n) = $\eqalign{\frac{8}{14}\cdot\frac{7}{13}\cdot\frac{6}{12}=\frac{2}{13}}$

Vervolgens kijk je hoeveel verschillende volgordes je kunt maken met twee witte en een niet-witte. Dit kan op 3 verschillende manieren, dus de kans op precies twee witte ballen is 3·$\eqalign{\frac{2}{13}=\frac{6}{13}}$

Uitwerking 3

Je kunt dit soort vragen ook oplossen door naar combinaties te kijken. Op hoeveel manieren kan je 2 witte knikkers uit de vaas halen.

$
P(2\,\,witte) = \frac{{\left( {\begin{array}{*{20}c}
   8  \\
   2  \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
   6  \\
   1  \\
\end{array}} \right)}}{{\left( {\begin{array}{*{20}c}
   {14}  \\
   3  \\
\end{array}} \right)}} \approx 0,462
$