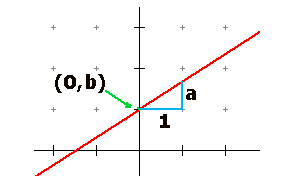1. Hoofdstuk 1 - lineaire problemen

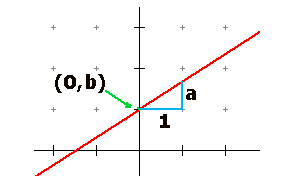
• Ik weet dat de formule $y=ax+b$ hoort bij de grafiek hiernaast.
• Ik kan bij een lineaire formule de grafiek tekenen.
  • Met een tabel
  • Met de richtingscoëfficiënt en het snijpunt met de $y$-as
  • Met de snijpunten met de $x$- en $y$-as.
• Ik kan voor een willekeurig punt controleren of het punt op een gegeven lijn ligt.
• Ik kan bij een gegeven punt de bijbehorende functiewaarde uitrekenen.
• Ik kan lineaire formules ook gebruiken bij andere letters dan $x$ en $y$.
• Ik kan de formule opstellen van een lijn bij een gegeven grafiek.
• Ik kan de formule opstellen van een lijn bij gegeven richtingscoëfficiënt een een punt.
• Ik kan de formule opstellen van een lijn door twee willekeurige punten.
• Ik weet dat bij evenwijdige lijnen de richtingscoëfficiënt hetzelfde is.
• Ik kan lineaire vergelijkingen oplossen, ook met haakjes en/of breuken.
• Ik kan de snijpunten van een lijn met de $x$- of $y$-as berekenen.
• Ik kan het snijpunt van twee lineaire grafieken berekenen.
• Ik weet wat er bedoeld wordt met origineel en beeld.
• Ik weet wat de haakjesnotatie is. Bijvoorbeeld: $f(x)=ax+b$.
• Ik kan bij vergelijkingen met twee variabelen de grafiek tekenen.
• Ik vergelijkingen met twee variabelen herleiden tot de standaardvorm $y=ax+b$.

• Er zijn drie manieren om grafieken te tekenen van lineaire formules. Een tabel maken was handig voor klas 1 en 2 maar in de 3e klas doe je dat anders, handiger.
• Als je richtingcoëfficiënt een breuk is dan moet je bedenken dat bijvoorbeeld $\frac{2}{5}$ hetzelfde is als '5 eenheden naar rechts,  2 omhoog....'.
• Om formules te maken bij een grafiek kijk je naar roosterpunten. De richtingscoëfficiënt is de verticale toename gedeeld door de horizontale toename.
• Bij de formule $y=ax+b$ is $a$ de richtingscoëfficiënt en $(0,b)$ het snijpunt met de $y$-as.

• lineaire problemen