Langs elke pijl neem je het produkt van de 3 getallen die langs deze pijl staan.
De produkten langs de blauwe pijlen tel je op, die langs de rode pijlen trek je er weer vanaf.
Een algemene manier om de determinant van een matrix te berekenen, vind je op:
Een vlotte manier om van een 3x3 matrix de determinant te berekenen, is de volgende:
Ga uit van de 3x3 matrix
$\left({\begin{array}{*{20}c}{a_1}&{a_2}&{a_3}\\{b_1}&{b_2}&{b_3}\\{c_1}&{c_2}&{c_3}\\\end{array}}\right)$
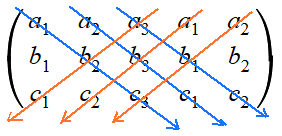
Breidt deze aan de rechterkant uit met de 1e twee kolommen:
$\left({\begin{array}{*{20}c}{a_1}&{a_2}&{a_3}&{a_1}&{a_2}\\{b_1}&{b_2}&{b_3}&{b_1}&{b_2}\\{c_1}&{c_2}&{c_3}&{c_1}&{c_2}\\\end{array}}\right)$
Tot slot teken (of denk) je 6 pijltjes zoals aangegeven:

Langs elke pijl neem je het produkt van de 3 getallen die langs deze pijl staan.
De produkten langs de blauwe pijlen tel je op, die langs de rode pijlen trek je er weer vanaf.
Dus: determinant= a1b2c3 + a2b3c1 + a3b1c2 - a3b2c1 - a1b3c2 - a2b1c3
Bij een 2x2 matrix is t nog wat eenvoudiger: determinant = a1b2 - a2b1
Groeten,
Martijn