Zie eventueel https://www.wiskundeleraar.nl en dan hulpmiddelen voor de hyperlink.
 met 5 voorbeelden op 1 pagina...
met 5 voorbeelden op 1 pagina...Er veel verschillende soorten functies:
Deze functies hebben karakteristieke eigenschappen: toppen, asymptoten, eindpunten, etc. Als je de grafiek van zo'n functie ziet kun je hem vaak gemakkelijk op grond van deze eigenschappen herkennen. Je kent al een aantal standaardfuncties waarvan je de karakteristieke eigenschappen kent. Veel grafieken zijn transformaties van die standaardgrafieken. Met behulp van die karakteristieke eigenschappen kan je bij gegeven grafieken het functievoorschrift opstellen.
Vraag 1
 met 5 voorbeelden op 1 pagina...
met 5 voorbeelden op 1 pagina...

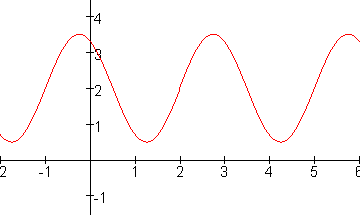
Kijk eerst naar het hoogste en laagste punt. Je weet dan de evenwichtsstand en de amplitude:
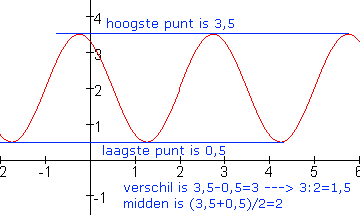
We zien: A=1,5 en c=2
Kijk dan naar de periode en t0:
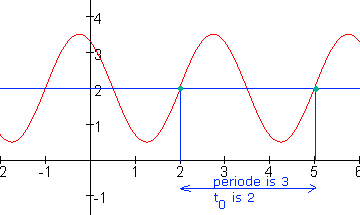
We zien T=3 en t0=2. De formule wordt:
Vraag 2
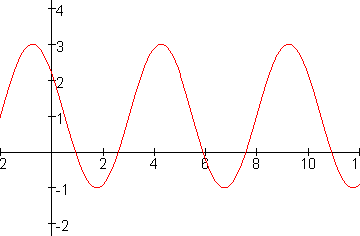
Vraag 3