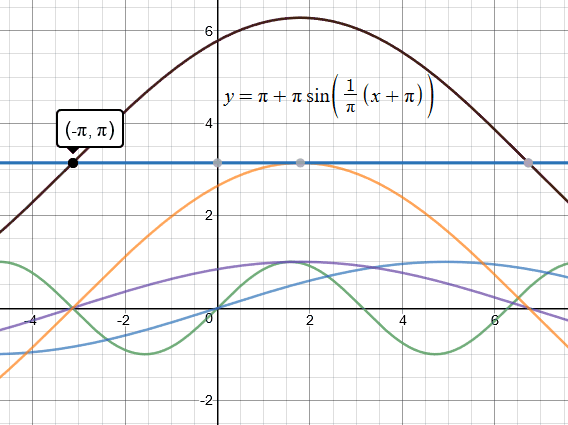Antwoorden
De eenheidscirkel
Vraag 1
-
30$^o$ immers $\frac{1}{6}\pi$ is $\frac{1}{6}$ van 180$^o$=30$^o$
-
$\frac{5}{6}\pi$, $2\frac{1}{6}\pi$ of $2\frac{5}{6}\pi$, maar ook $-1\frac{1}{6}\pi$ of $-1\frac{1}{6}\pi$, enz.
-
De sinus van $8\frac{5}{6}\pi$ is gelijk aan $\frac{1}{2}$. Het is immers modulo $2\pi$.
-
$\cos(1\frac{3}{4}\pi)=\frac{1}{2}$ en $\cos(-\frac{1}{4}\pi)=\frac{1}{2}$. Deze hoeken zijn niet gelijk aan elkaar.
-
Dat is onzin. Er zijn oneindig veel hoeken met dezelfde waarde van de sinus.
Vraag 2
-
$\sin(\frac{2}{3}\pi)=\frac{1}{2}\sqrt{3}$ en $\cos(\frac{2}{3}\pi)=-\frac{1}{2}$.
-
Dat is $\frac{1}{4}\pi$.
-
Dat is geen toeval...
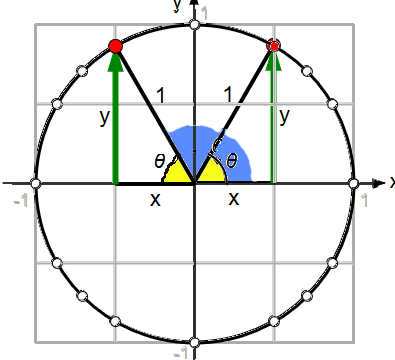
Als de gele hoek gelijk is aan $a$ dan is de blauwe hoek gelijk aan $\pi-a$ en dat is samen gelijk aan $\pi$.
-
Je weet dan dat $\alpha+\beta=\pi+k\cdot2\pi$ met $k=\{..., -2, -1, 0, 1, 2, ....\}$
-
Je weet dan dat $\alpha+\beta=k\cdot2\pi$ met $k=\{..., -2, -1, 0, 1, 2, ....\}$
Vraag 3
-
$\sin \left( \alpha \right) = \frac{1}{2}\sqrt 3 \Rightarrow \alpha = \frac{1}{3}\pi + k \cdot 2\pi \vee \alpha = \frac{2}{3}\pi + k \cdot 2\pi $. Er zijn twee oneindige verzamelingen van oplossingen.
-
Zie a.
-
$\cos \left( \beta \right) = \frac{1}{2}\sqrt 3 \Rightarrow \beta = \frac{1}{6}\pi + k \cdot 2\pi \vee \beta = - \frac{1}{6}\pi + k \cdot 2\pi $
Vraag 4
-
$\cos \left( \alpha \right) = \frac{1}{2} \Rightarrow \alpha = \frac{1}{3}\pi + k \cdot 2\pi \vee \alpha = - \frac{1}{3}\pi + k \cdot 2\pi $
-
$\sin \left( \alpha \right) = - \frac{1}{2}\sqrt 2 \Rightarrow \alpha = 1\frac{1}{4}\pi + k \cdot 2\pi \vee \alpha = 1\frac{3}{4}\pi + k \cdot 2\pi $
-
$\sin \left( \alpha \right) = 0 \Rightarrow \alpha = k \cdot \pi $
-
$\cos \left( \alpha \right) = 1 \Rightarrow \alpha = k \cdot 2\pi $
-
$\sin \left( \alpha \right) = - 1 \Rightarrow \alpha = 1\frac{1}{2}\pi + k \cdot 2\pi $
-
$\sin \left( \alpha \right) = \cos \left( {2\frac{1}{2}\pi } \right) \Rightarrow \sin \left( \alpha \right) = 0 \Rightarrow \alpha = k \cdot \pi $
Grafieken van goniometrische functies
-
de evenwichtsstand=2, de amplitude=3, de periode=3 en de verticale verschuiving is 2
-
er geldt $d=\frac{1}{2}$, je moet kijken naar $-\sin(...)$ en die 'start' in het punt $(\frac{1}{2},2)$
-
$g(x)=3+2\cdot\sin(\frac{2\pi}{6}(x+1))$
-
$y=-1-3\cdot\sin(\frac{3\pi}{7}(x+2)$
Karakteristieke eigenschappen
Vraag 2
-
$y=1+2\cdot\sin(\frac{2\pi}{5}(x-3))$
-
$y=1-2\cdot\sin(\frac{2\pi}{5}(x-\frac{1}{2}))$
-
$y=1+2\cdot\cos(\frac{2\pi}{5}(x-4\frac{1}{4}))$
Transformaties van grafieken
Opdracht 1
$y = \sin (x)$
-
Vermenigvuldigen met $\frac{1}{3}$ t.o.v. de $y$-as:
$y = \sin (3x)$
-
verschuif de grafiek 1 naar rechts:
$y = \sin (3(x - 1))$
-
vermenigvuldig met $-3$ t.o.v. de $x$-as:
$y = - 3 \cdot \sin (3(x - 1))$
-
verschuif de grafiek 2 omhoog:
$y = 2 - 3 \cdot \sin (3(x - 1))$
De evenwichtsstand is: y=2, de amplitude is 3 (niet -3), de periode is $\frac{2\pi}{3}$ en de coördinaten van het beginpunt zijn (1,2)
Opdracht 2
$\eqalign{y = \pi + \pi \cdot \sin \left( {\frac{1}{\pi }\left( {x + \pi } \right)} \right)}$
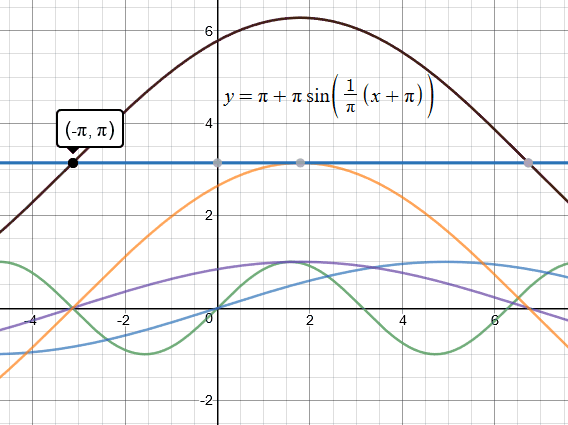
Goniometrische vergelijkingen oplossen
Opdracht
-
$
\sqrt 2 \cdot \sin (2x - \pi ) = 1
$
$
\sin (2x - \pi ) = \frac{1}{2}\sqrt 2
$
$
2x - \pi = \frac{1}{4}\pi + k \cdot 2\pi
$ of $
2x - \pi = \frac{3}{4}\pi + k \cdot 2\pi
$
$
2x = 1\frac{1}{4}\pi + k \cdot 2\pi
$ of $
2x = 1\frac{3}{4}\pi + k \cdot 2\pi
$
$
x = \frac{5}{8}\pi + k \cdot \pi
$ of $
x = \frac{7}{8}\pi + k \cdot \pi
$
-
$
2\cos \left( {2x - \frac{1}{3}\pi } \right) = \sqrt 3
$
$
\cos \left( {2x - \frac{1}{3}\pi } \right) = \frac{1}{2}\sqrt 3
$
$
2x - \frac{1}{3}\pi = \frac{1}{6}\pi + k \cdot 2\pi
$ of $
2x - \frac{1}{3}\pi = - \frac{1}{6}\pi + k \cdot 2\pi
$
$
2x = \frac{1}{2}\pi + k \cdot 2\pi
$ of $
2x = \frac{1}{6}\pi + k \cdot 2\pi
$
$
x = \frac{1}{4}\pi + k \cdot \pi
$ of $
x = \frac{1}{{12}}\pi + k \cdot \pi
$
-
$
\sin (x)\cos (x) - \sin (x) = 0
$
$
\sin (x)\left( {\cos (x) - 1} \right) = 0
$
$
\sin (x) = 0
$ of $
\cos (x) - 1 = 0
$
$
x = k \cdot \pi
$ of $
\cos (x) = 1
$
$
x = k \cdot \pi
$ of $
x = \frac{1}{2}\pi + k \cdot \pi
$
$
x = k \cdot \frac{1}{2}\pi
$
-
$
\sin ^2 (x) = \frac{1}{2}
$
$
\sin (x) = - \sqrt {\frac{1}{2}}
$ of $
\sin (x) = \sqrt {\frac{1}{2}}
$
$
\sin (x) = - \frac{1}{2}\sqrt 2
$ of $
\sin (x) = \frac{1}{2}\sqrt 2
$
$
x = 1\frac{1}{4}\pi + k \cdot 2\pi
$ of $
x = 1\frac{3}{4}\pi + k \cdot 2\pi
$ of $
x = \frac{1}{4}\pi + k \cdot 2\pi
$ of $
x = \frac{3}{4}\pi + k \cdot 2\pi
$
$
x = \frac{1}{4}\pi + k \cdot \frac{1}{2}\pi
$
Toepassingen en probleemaanpak
Opdracht 1
-
$\eqalign{h = 22 + 20 \cdot \sin \left( {\frac{{2\pi }}{{60}}t} \right)}$
Opdracht 2
-
De evenwichtslijn: $a=\frac{25+9}{2}=17$
-
De amplitude: $b=25-17=8$
-
De periode is 365 dagen. Dus $c=\frac{2\pi}{365}$
-
'Stijgend door de evenwichtsstand' op 91 dagen voor $T_{max}$.
$d=201-91=110$
...finito...!
De formule:
-
$
\eqalign{T = 17 + 8 \cdot \sin \left( {\frac{{2\pi }}{{365}}\left( {n - 110} \right)} \right)}
$
Opdracht 3
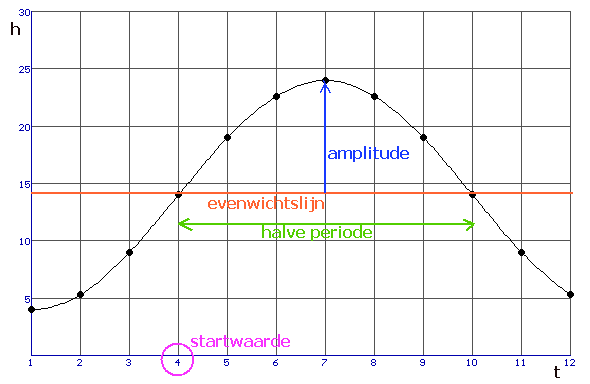
Bij benadering:
-
$a=14$
-
$b=10$
-
$\eqalign{c=\frac{2\pi}{12}}$
-
$d=4$
De formule wordt:
$
\eqalign{h(t) = 14 + 10\sin \left( {\frac{{2\pi }}{{12}}\left( {t - 4} \right)} \right)}
$