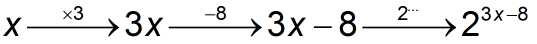
Inverse functies

Neem aan dat je een functie hebt met als functievoorschrift $f(x)=2^{3x-8}$. Je kunt met zo'n functievoorschrift de functiewaarde uitrekenen voor verschillende waarden van $x$.

$f(3)=2^{3·3-8}=2^{1}=2$
$f(4)=2^{3·4-8}=2^{4}=16$
$f(5)=2^{3·5-8}=2^{7}=128$

De vraag is nu of er een functie te bedenken is waarmee je bij een gegeven waarde van $y$ de bijbehorende waarden van $x$ kan berekenen. Je kunt bij een gegeven $y$ proberen de waarde van $x$ te vinden door op de $y$ in omgekeerde volgorde de inverse bewerkingen toe te passen. Bedenk daarbij:

• de inverse bewerking van optellen is aftrekken
• de inverse bewerking van vermenigvuldigen is delen
• de inverse bewerking van kwadrateren is worteltrekken (op een beperkt domein)
• de inverse bewerking van $g^{...}$ is $\,^g log(...)$
• de inverse bewerking van $\eqalign{g^{a}}$ is $\eqalign{g^{\frac{1}{a}}}$

Voorbeeld

Kijk nog 's naar $f(x)=2^{3x-8}$. Gegeven: $f(x)=1024$. Wat is $x$?

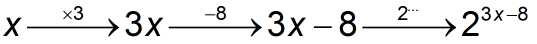
Nu van achter naar voren de inverse bewerkingen toepassen op $y$:

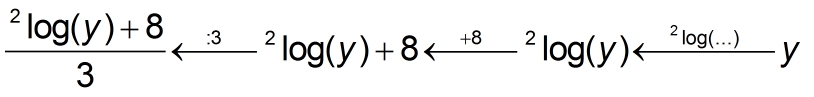
We zien dat met $y=2^{3x-8}$ de inverse functie gelijk is aan $\eqalign{x=\frac{^2\log(y)+8}{3}}$.

Dus als $y=1024$ dan:

• $\eqalign{x=\frac{^2\log(1024)+8}{3}}$
• $\eqalign{x=\frac{10+8}{3}}$
• $\eqalign{x=\frac{18}{3}}$
• $\eqalign{x=6}$

Opgave 25

Om $x$ te berekenen had je, in bovenstaand voorbeeld ook de vergelijking $2^{3x-8}=1024$ kunnen oplossen.

• Los de vergelijking op.
• Valt je iets op?

Om de inverse te vinden van bijvoorbeeld $y=\sqrt{3x-2}+5$ kan je ook proberen om $x$ uit te drukken in $y$. Vervang vervolgens de 'x' door 'y' en de 'y' door 'x' en je bent er...

Opgave 26

• Gegeven $y=\sqrt{3x-2}+5$. Druk $x$ uit in $y$.

Opgave 27

Open http://www.wisbe.nl/inverse.htm en bekijk de grafieken en hun inverse.

• Wat is de inverse van $\eqalign{y=\frac{1}{x}}$?

Opgave 28

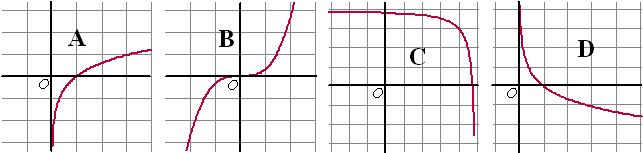
Schets de grafieken van de inversen van de volgende functies:

http://hhofstede.nl

Opgave 29

Druk $x$ uit in $y$:

1. $y=3x-1$
2. $y=2+\sqrt{4x-6}$
3. $y=4x^3-9$
4. $y=\,^2\log(4-3x)-2$
5. $y=1+2^{4x+7}$