Antwoorden

Opgave 1

1. $
   y = \frac{2}
   {5}x + 1\frac{4}
   {5}
   $
2. Het snijpunt met de y-as is (0,-4) en het snijpunt met de x-as is (1$\frac{1}{3}$,0)
3. $(\frac{4}{5},1\frac{2}{5})$

Opgave 2

• $f(x)=1\frac{1}{4}(x+2)-2$ geeft $y=1\frac{1}{4}x+\frac{1}{2}$
• $f(x)=1\frac{1}{4}(x-2)+3$ geeft $y=1\frac{1}{4}x+\frac{1}{2}$

Opgave 3

• De richtingscoëfficient van de lijn is $-\frac{2}{3}$ dus dat is vast goed. Als je de coördinaten van $A(5,-2)$ invult dan kan je constateren van $A$ op de lijn ligt. In dat geval moet dit wel een goede vergelijking zijn.

Opgave 4

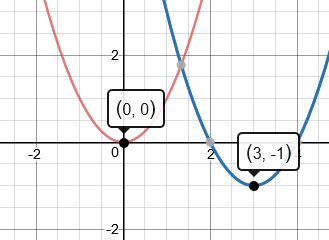
De coördinaten van de toppen zijn:

1. $\left( {4,4} \right)$
2. $\left( {-3,-11} \right)$
3. $\left( {-1\frac{1}{2},2\frac{3}{4}} \right)$
4. $\left( {0,3} \right)$
5. $\left( {-7,0} \right)$

Opgave 5

1. De top is $(1,-2)$
2. Als $a\gt0$ dan is de parabool een dalparabool. Als $a\lt0$ dan is het een bergparabool. Als $a$ groter wordt dan wordt de parabool smaller. Tussen $0$ en $1$ of tussen $-1$ en $0$ wordt de parabool wijder.
3. Neem $a=\frac{5}{36}$. Ga na!
4. $y=3$ voor $x=-4$ of $x=6$.
   Je kunt dat berekenen door het oplossen van de vergelijking $\frac{1}{5}(x-1)^2-2=3$.
   $\eqalign{
     & \frac{1}{5}{\left( {x - 1} \right)^2} - 2 = 3  \cr
     & \frac{1}{5}{(x - 1)^2} = 5  \cr
     & {(x - 1)^2} = 25  \cr
     & x - 1 =  - 5 \vee x - 1 = 5  \cr
     & x =  - 4 \vee x = 6 \cr} $

Opgave 6

Opgave 7

Dat is de vector $(-5,2)$

Je kunt dat ook berekenen:

$\begin{array}{l}
y = {x^2} - 4x + 2 \to y = {(x - 2)^2} - 2\\
y = {x^2} + 6x + 5 \to y = {(x + 3)^2} - 4
\end{array}$

Van $\left( {2, - 2} \right)$ naar $\left( { - 3, - 4} \right)$ geeft $(-5,-2)$.

Opgave 8

Vervang in $y =  - {x^2} + 5x + 5$ de $x$ door $(x+2)$ en tel $6$ op bij het functievoorschrift. Je krijgt dan:

$\begin{array}{l}
y =  - {(x + 2)^2} + 5(x + 2) + 5 + 6\\
y =  - ({x^2} + 4x + 4) + 5x + 10 + 11\\
y =  - {x^2} - 4x - 4 + 5x + 21\\
y =  - {x^2} + x + 17
\end{array}$

Opgave 9

1. $x =  - \sqrt[4]{5} \vee x = \sqrt[4]{5}$
2. $x = \sqrt[5]{5}$
3. $x =  - \sqrt[6]{\pi } \vee x = \sqrt[6]{\pi }$
4. geen oplossing

Opgave 10

• vermenigvuldigen met $-2$ t.o.v. $x$-as
• transleren over de vector $(-3, 5)$

Opgave 11

• $y = \frac{1}{2}{\left( {x - 2} \right)^5} - 3$

Opgave 12

• De volgorde is wel van belang. Als je op $y = {x^5}$ eerst de translatie(s) toepast en daarna de verminigvuldiging dan krijg je:
  • $y = {x^5}$
  • $y = {\left( {x - 2} \right)^5} - 3$
  • $y = \frac{1}{2}{\left( {x - 2} \right)^5} - 1\frac{1}{2}$
• ...en dat is niet hetzelfde.

Opgave 13

• standaardfunctie: $f(x) = {2^x}$
• vermenigvuldigen met de factor $4$ t.o.v. de x-as geeft: $f(x) = 4 \cdot {2^x}$
• $1$ naar rechts verschuiven geeft: $f(x) = 4 \cdot {2^{x - 1}}$
• $3$ verschuiven naar beneden geeft: $f(x) = 4 \cdot {2^{x - 1}} - 3$

Opgave 14

Opgave 15

Opgave 16

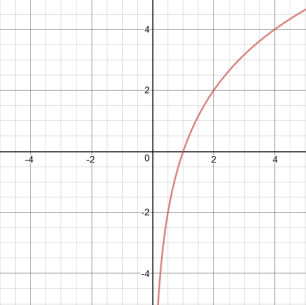
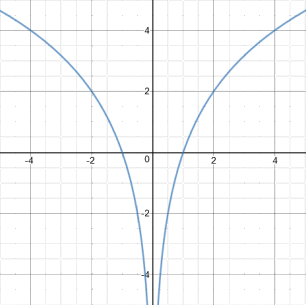
De logaritme $^2log(x)$ is alleen gedefinieerd voor $x\gt0$. Bij de linker grafiek heb je daarom alleen punten voor $x\gt0$. Bij de rechter grafiek heb je links ook een tak.

Opgave 17

$\eqalign{
  & 2 + \frac{8}{{x + 3}} = 2x + 2  \cr
  & \frac{8}{{x + 3}} = 2x  \cr
  & 2x(x + 3) = 8  \cr
  & 2{x^2} + 6x = 8  \cr
  & {x^2} + 3x = 4  \cr
  & {x^2} + 3x - 4 = 0  \cr
  & (x + 4)(x - 1) = 0  \cr
  & x =  - 4 \vee x = 1  \cr
  & ( - 4, - 6)\,\,en\,\,(1,4) \cr} $

Opgave 18

$\eqalign{f(x) = \frac{1}{x}}$

vermenigvuldigen met $8$ t.o.v. de $y$-as

$\eqalign{f(x) = \frac{8}{x}}$

translatie over $(-3,2)$

$\eqalign{f(x) = 2 + \frac{8}{x + 3}}$

Opgave 19

1. $\eqalign{y=1+\frac{1}{x-5}}$
2. $\eqalign{y=-2+\frac{2}{x-1}}$
3. $\eqalign{y=1-\frac{1}{2(x-4)}}$

Opgave 20

$\eqalign{
  & f(x) = \frac{2}{{x - 3}} + 4  \cr
  & f(x) = \frac{2}{{\left( {\frac{1}{2}x} \right) - 3}} + 4 \to f(x) = \frac{4}{{x - 6}} + 4  \cr
  & f(x) = \frac{4}{{\left( {x + 3} \right) - 6}} + 4 \to f(x) = \frac{4}{{x - 3}} + 4  \cr
  & f(x) = \frac{2}{{x - 3}} + 2 \cr} $

Opgave 21

Gegeven: $f(x)=-2\sqrt{-x-1}+3$
Gevraagd: domein en bereik

• Het startpunt is $(-1,3)$
• De grafiek loopt naar links
• De grafiek loopt omlaag

Het domein is $<\leftarrow,-1]$
Het bereik is $<\leftarrow,3]$

Opgave 22

$
\eqalign{
  & f(x) = g(x)  \cr
  & \sqrt x  = 2\sqrt {x - 3}   \cr
  & x = 4\left( {x - 3} \right)  \cr
  & x = 4x - 12  \cr
  &  - 3x =  - 12  \cr
  & x = 4 \cr}
$

Contoleer je oplossing. $x=4$ voldoet.
Met f(4)=2 krijg je $A(4,2)$.

Opgave 23

1. $
    3x - 5\sqrt x  - 2 = 0
   $
   $
   \eqalign{
   & -5\sqrt x  =  - 3x + 2  \cr
   & 25x = ( - 3x + 2)^2   \cr
   & 25x = 9x^2  - 12x + 4  \cr
   & 9x^2  - 37x + 4 = 0  \cr
   & 9x^2  - 36x - x + 4 = 0  \cr
   & 9x(x - 4) - (x - 4) = 0  \cr
   & (9x - 1)(x - 4) = 0  \cr
   & 9x = 1 \vee x = 4  \cr
   & x = \frac{1}
   {9}(v.n.) \vee x = 4  \cr
   & x = 4 \cr}
   $
2. $
   x  -4\sqrt x  + 2 = 0
   $
   $
   \eqalign{
   & -4\sqrt x  =  - x - 2  \cr
   & 4\sqrt x  = x + 2  \cr
   & 16x = x^2  + 4x + 4  \cr
   & x^2  - 12x + 4 = 0  \cr
   & (x - 6)^2  - 36 + 4 = 0  \cr
   & (x - 6)^2  = 32  \cr
   & x - 6 =  \pm \sqrt {32}   \cr
   & x = 6 \pm 4\sqrt 2   \cr
   & x = 6 - 4\sqrt 2  \vee x = 6 + 4\sqrt 2  \cr}
   $
3. $
    6x + \sqrt x  = 7x - 20
   $
   $
   \eqalign{
   & \sqrt x  = x - 20  \cr
   & x = x^2  - 40x + 400  \cr
   & x^2  - 41x + 400 = 0  \cr
   & (x - 16)(x - 25) = 0  \cr
   & x = 16(v.n.) \vee x = 25  \cr
   & x = 25 \cr}
   $

Opgave 24

$
\eqalign{
  & K = 4 + \sqrt {3p + 1}   \cr
  & K - 4 = \sqrt {3p + 1}   \cr
  & \left( {K - 4} \right)^2  = 3p + 1  \cr
  & \left( {K - 4} \right)^2  - 1 = 3p  \cr
  & p = \frac{1}
{3}\left( {K - 4} \right)^2  - \frac{1}
{3} \cr}
$

Opgave 25

$\eqalign{
  & {2^{3x - 8}} = 1024  \cr
  & {}^2\log \left( {{2^{3x - 8}}} \right) = {}^2\log \left( {1024} \right)  \cr
  & 3x - 8 = 10  \cr
  & 3x = 18  \cr
  & x = 6 \cr} $

Opgave 26

$\eqalign{
  & y = \sqrt {3x - 2}  + 5  \cr
  & \sqrt {3x - 2}  = y - 5  \cr
  & 3x - 2 = {\left( {y - 5} \right)^2}  \cr
  & 3x = {\left( {y - 5} \right)^2} + 2  \cr
  & x = \frac{{{{\left( {y - 5} \right)}^2} + 2}}{3} \cr} $

Opgave 27

De inverse van $\eqalign{y=\frac{1}{x}}$ is $\eqalign{y=\frac{1}{x}}$.

Opgave 28

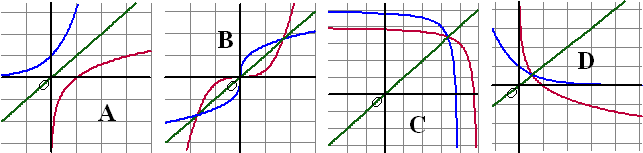
Opgave 29

1. $\eqalign{x = \frac{{y + 1}}{3}}$
2. $\eqalign{x = \frac{1}{4}{(y - 2)^2} + 1\frac{1}{2}}$
3. $\eqalign{x = \root 3 \of {\frac{{y + 9}}{4}}}$
4. $\eqalign{x =  - \frac{{{2^{4 - 3x}}}}{3}}$
5. $\eqalign{x = \frac{1}{4} \cdot {}^2\log (y - 1) - 1\frac{3}{4}}$