kwadraatafsplitsen

Stel je voor dat ik van een rechthoek met zijden $x$ en $x+4$ een vierkant wil maken.
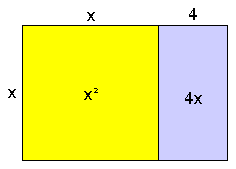Ik verdeel daarvoor het stuk van $4x$ is twee stukken van $2x$ en leg ze netjes aan weerzijden van het vierkant $x^{2}$. Dan heb ik al bijna een vierkant met zijde $x+2$.
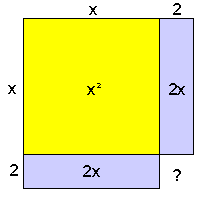Maar 't klopt niet helemaal. Eigenlijk kom ik een stukje van $4$ tekort. Maar bijna goed...:-)

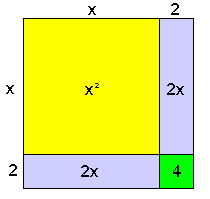Eigenlijk heb ik geprobeerd om $x^{2}+4x$ te schrijven als een kwadraat. Dat ging 'bijna' goed, maar niet helemaal. Als je 't schrijft als formules dan krijg je zoiets als:

$x^{2}+4x=(x+2)^{2}-4$

Die $4$ is dan dat stukje dat ik tekort kwam.

Ga na dat $(x+2)^{2}-4$ gelijk is aan $x^{2}+4x$

Kwadraatafsplitsen

Zoiets kan je ook doen voor bijvoorbeeld $x^2+6x+5$. Ik maak er $(x+3)^{2}-9+5$ van. Die $9$ komt van $3^{2}$, zodat je kunt schrijven:

$x^2+6x+5=(x+3)^{2}-9+5=(x+3)^{2}-4$

We zeggen dan dat we een kwadraat hebben afgesplitst.

Voorbeelden

Je ziet hier een aantal voorbeelden van kwadraatafsplitsen:

$
\begin{array}{l}
x^2 - 8x + 2 = (x - 4)^2 - 16 + 2 = (x - 4)^2 - 14 \\
x^2 + 4x + 4 = (x + 2)^2 -4 + 4 = (x + 2)^2 \\
x^2 - 12x = \left( {x - 6} \right)^2 - 36 \\
\end{array}
$
Ga na dat het klopt!

Welke antwoorden zijn juist?

$
x^2 + 10x - 20
$ geeft:

$(x + 5)^2 - 5$

$(x + 5)^2 - 25$

$(x + 5)^2 - 45$

$
x^2 - 2x + 2
$ geeft:

$(x - 1)^2$

$(x - 1)^2-1$

$(x - 1)^2 + 1$

$(x - 1)^2 + 3$

Topformule

De grafiek van $y = a\left( {x - p} \right)^2 + q$ heeft als top $\left( {p,q} \right)$.

Voorbeelden

Geef de coördinaten van de top van deze parabolen:

$y=x^{2}-4x-5$
$y=x^{2}+8x+10$
$y=x^{2}+6x+12$

Uitgewerkt

$y=(x-2)^{2}-9$. De top is $(2,-9)$
$y=(x+4)^{2}-6$. De top is $(-4,-6)$
$y=(x+3)^{2}+3$. De top is $(-3,3)$

Vergelijkingen oplossen

Je kunt kwadraatafsplitsen gebruiken om tweedegraads-vergelijkingen op te lossen.

Voorbeeld 1

$ \begin{array}{l}
x^2 + 4x - 12 = 0 \\
(x + 2)^2 - 4 - 12 = 0 \\
(x + 2)^2 - 16 = 0 \\
(x + 2)^2 = 16 \\
x + 2 = - 4 \vee x + 2 = 4 \\
x = - 6 \vee x = 2 \\
\end{array} $

Als de wortel niet 'leuk' uitkomt kan je de vergelijking nog steeds oplossen met kwadraatafspliten.

Voorbeeld 2

$
\begin{array}{l}
x^2 + 4x - 2 = 0 \\
(x + 2)^2 - 6 = 0 \\
(x + 2)^2 = 6 \\
x + 2 = - \sqrt 6 \vee x + 2 = \sqrt 6 \\
x = - 2 - \sqrt 6 \vee x = - 2 + \sqrt 6 \\
\end{array}
$

De cirkelvergelijking

Voor het herleiden van de vergelijking $x^2+y^2-4x+6y-3=0$ tot de vorm $(x-2)^2+(y+3)^2=16$ gebruik je de techniek van het kwadraatafsplitsen.

Voorbeeld

Wat is het middelpunt en de straal van de cirkel met vergelijking $x^2+y^2+8x-2y+6=0$?

Uitwerking

$x^2+y^2+8x-2y+6=0$
$x^2+8x+y^2-2y+6=0$
$(x+4)^2-16+(y-1)^2-1+6=0$
$(x+4)^2+(y-1)^2-11=0$
$(x+4)^2+(y-1)^2=11$

Het middelpunt is $M(-4,1)$ en de straal is $r=\sqrt{11}$