Vraag:

Neem aan dat je een lijn $k$ hebt met richtingscoëfficiënt $\frac{3}{4}$. Wat is dan de richtingscoëfficiënt van de lijn $m$ die loodrecht op $k$ staat?

Antwoord:

Er geldt: $rc_k·rc_m=-1$. Invullen geeft:

$
\eqalign{
  & \frac{3}
{4} \cdot rc_m  =  - 1  \cr
  & 3 \cdot rc_m  =  - 4  \cr
  & rc_m  =  - \frac{4}
{3} \cr}
$

Je kunt ook zeggen dat de richtingscoëfficiënt van $m$ omgekeerd en tegengesteld is.

Je kunt de vergelijkingen van een lijn ook geven in de vorm $k:ax+by=c$. Wat is dan de vergelijking van de lijn $m$ die loodrecht staat op $k$?

Je draait dan de coëfficiënten om en neemt er één tegengesteld.
Neem $m:bx-ay=d$

Voorbeeld

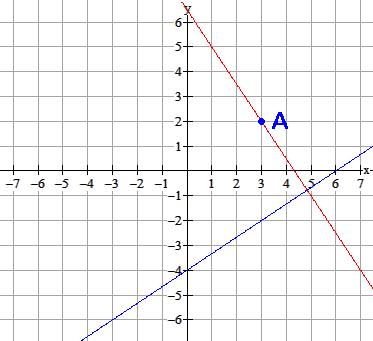
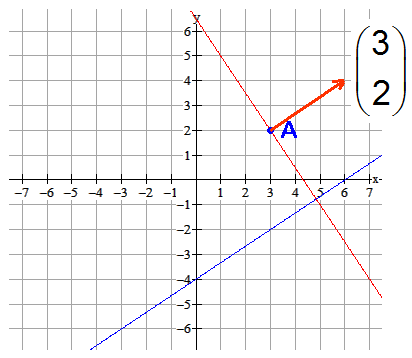
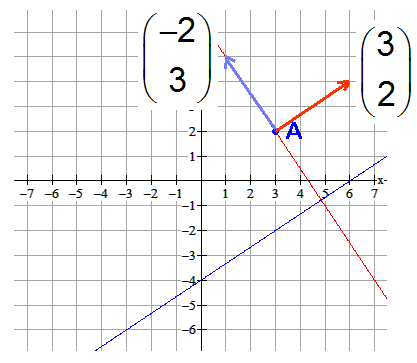
Gegeven $k:2x-3y=12$. Geef de vergelijking van lijn $m$ die loodrecht staat op $k$ en door het punt $A(3,2)$ gaat.

Uitwerking

De lijn $m$ heeft als vergelijking $m:3x+2y=c$. Vul $A(3,2)$ in. Je krijgt $c=3.3+2·2=13$.
De vergelijking is $m:3x+2y=13$

Je kun dat ook zo zien:

Eerst ging je $3$ naar rechts $2$ omhoog. Draaien over $90^o$ geeft de richting loodrecht op $k$ en dat is dan $3$ omhoog en $2$ naar links, oftwel $-2$ naar rechts en $3$ omhoog en zoals je ziet draaien de kentallen van de vector om en wordt het eerste kental negatief.

• Omgekeerd en tegengesteld.

Neem aan dat de richtingscoëficiënt van lijn $k$ gelijk is aan $a$. Wat is dat de richtingscoëfficiënt van $m$ als $m$ loodrecht staat op $k$?

$
\begin{array}{l}
 rc_k  = a \equiv \left( {\begin{array}{*{20}c}
   1  \\
   a  \\
\end{array}} \right) \to \left( {\begin{array}{*{20}c}
   { - a}  \\
   1  \\
\end{array}} \right) \equiv  - a = rc_m  \\
 rc_k  \cdot rc_m  =  - 1 \\
 \end{array}
$