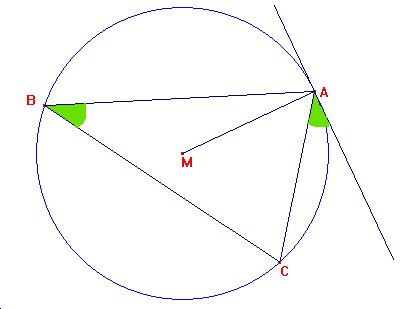

De hoek tussen een raaklijn aan een cirkel en een koorde van die cirkel waarvan een eindpunt het raakpunt is, is even groot als de bij die koorde behorende omtrekshoek. (stelling hoek tussen koorde en raaklijn)
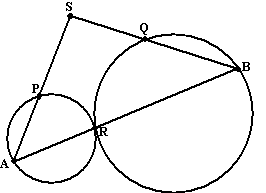
Twee cirkels raken elkaar in R. Een lijn door R snijdt de cirkels in A en in B. S is een willekeurig punt buiten de cirkels. SA en SB snijden de cirkels in P en Q.
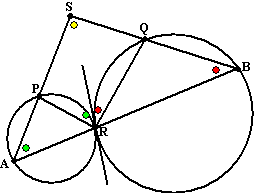
De rode hoeken zijn gelijk (koorde en raaklijn).
De groene hoeken zijn gelijk (koorde en raaklijn)
rood + groen + geel = 180º (hoekensom driehoek ABS)
dus ∠PSQ + ∠PRQ = 180º
Dan is PQRS een koordenvierhoek.
Dan liggen de punten P, Q, R en S op één cirkel.