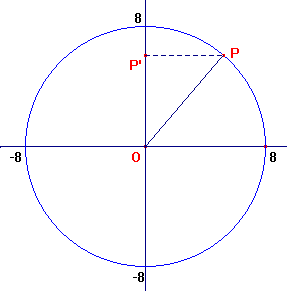
Als het punt P met een constante snelheid de cirkel doorloopt dan beschrijft P' (de projectie van P op de y-as) een harmonische trilling.De periode of trillingstijd bij een repeterend verschijnsel is de tijdsduur tussen twee opeenvolgende gebeurtenissen waarbij de fysische toestand gelijk is. De periode T is het omgekeerde van de frequentie f, en wordt in het SI-stelsel in seconden uitgedrukt.
Zodoende geldt:
$\eqalign{T=\frac{1}{f}}$
Als het punt P met een constante snelheid de cirkel doorloopt dan beschrijft P' (de projectie van P op de y-as) een harmonische trilling.
Neem aan dat het punt P in 10 seconden rond draait en dat de straal van de cirkel 8 is. De trillingstijd T is dan 10 seconden. Als op t=0 het punt P op (8,0) is dan hoort bij de harmonische beweging van P' deze formule:
$
\Large y_{P'} = 8 \cdot \sin \left( {\frac{{2\pi }}{{10}}t} \right)
$
De frequentie $f$ is het aantal trillingen per seconde:
$f=\frac{1}{T}=\frac{1}{10}$ hertz.
Geef een functie die varieert tussen 8 en -2 volt met frequentie 20 Hertz en startwaarde 0.
$\eqalign{a=\frac{8+-2}{2}=3}$
$\eqalign{b=\frac{8--2}{2}=5}$
$\eqalign{T=\frac{1}{f}=\frac{1}{20}}$
$\eqalign{c=\frac{2\pi}{T}=40\pi}$
$d=0$
$h(t)=3+5\cdot sin(40\pi\cdot t)$