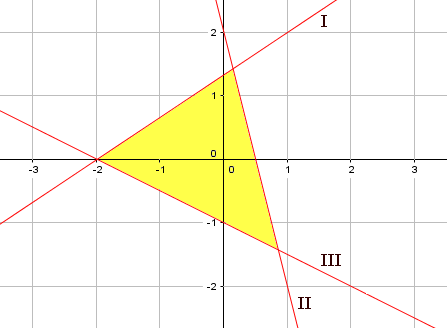
Voorbeeld 2

In voorbeeld 2 zie je 3 lijnen lopen. In hoofdstuk 5 had je al kennis gemaakt met formules voor rechte lijnen.
Hier zou je dan moeten proberen de formules voor de lijnen te vinden en te bepalen of het gebied hoort bij 'groter dan' of bij 'kleiner dan'. Dat is nog wel een lastig klusje. Op de website staat een soort van samenvatting maar niet hoe je dat doet.
Lijn I
Lijn I gaat door (-2,0) en (1,2). Vorig jaar heb je geleerd hoe je een formule van een rechte lijn kunt opstellen aan de hand van twee gegeven punten. Richtingscoëfficiënt en het snijpunt met de y-as:
In dit geval gaat dat zo:
$ \eqalign{ & a = \frac{{y_A - y_B }} {{x_A - X_B }} = \frac{{0 - 2}} {{ - 2 - 1}} = \frac{{ - 2}} {{ - 3}} = \frac{2} {3} \cr & y = \frac{2} {3}x + b \cr & {\text{Vul}}\,\,{\text{(1}}{\text{,2)}}\,\,{\text{in}}\,{\text{:}} \cr & 2 = \frac{2} {3} \cdot 1 + b \Rightarrow b = 1\frac{1} {3} \cr & {\text{Formule}}\,\,{\text{van}}\,\,{\text{lijn}}\,\,{\text{I:}}y = \frac{2} {3}x + 1\frac{1} {3} \cr} $
Je kunt nu de formule 'omwerken' tot '...x+...y=...'. Dat gaat zo:
$ \eqalign{ & y = \frac{2} {3}x + 1\frac{1} {3} \cr & 3y = 2x + 4 \cr & - 2x + 3y = 4 \cr & 2x - 3y = - 4 \cr} $
De vraag is dan of het $\ge$ of $\le$ moet zijn. Als je O(0,0) invult dan komt er $0$ uit en dat is groter dan $-4$ dus:
$ 2 \cdot 0 - 3 \cdot 0 = 0 \Rightarrow 2x - 3y \geq - 4 $
Je hebt nu de ongelijkheid die hoort bij lijn I. Op dezelfde manier kan je dat voor lijn II en III doen.