Tips en truuks - opgaven

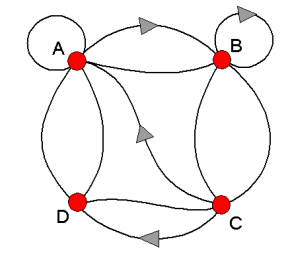
Opgave 0.

Los op:

• $ 0,125^{2x} = \sqrt {32}$

Opgave 1.

Vul in:

• $81x^4-x^4y^8=(....+.....)(....-....)(....+.....)$

Opgave 2.

• Een vat met olie weegt 58 kg. Een vat tot 70 procent gevuld weegt 43 kg. Hoeveel weegt het vat?

Opgave 3.

• Een vader, zijn zoon en zijn dochter zijn samen 44 jaar. De vader is viermaal zo oud als de zoon en deze laatste is tweemaal zo oud als de dochter. Hoe oud is iedereen?

Opgave 4.

• Hoeveel routes zijn er om in drie stappen van C naar A te gaan?

Opgave 5.

Het koken van 4 eieren duurt 6 minuten.

• Hoelang duurt het koken van 7 eieren?

Opgave 6.

• bereken de inhoud van het prisma.

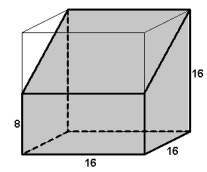
Opgave 7.

Het leger van koning Willem I bestaat uit ridders te paard en strijders te voet. Er zijn 100 man en 316 benen.

• Uit hoeveel ridders te paard bestaat dit leger?

Opgave 8.

• Construeer een vlak V welke gaat door het punt P (dat op BT ligt), zo dat de doorsnede van V met piramide T.ABCD een parallellogram is.

Opgave 9.

Gegeven: $
\cos \left( {2\pi t} \right) = \cos \left( {\frac{1}
{6}\pi t} \right)
$

• Los op voor $t\in [0,\pi]$

Opgave A1.

Twaalf vrienden trekken er een dagje op uit met de wagen. Er zijn 3 wagens beschikbaar.

• Op hoeveel manieren kan je drie groepjes van 4 maken?

Opgave A2.

Een groep van 24 studenten moet verdeeld worden in 3 even grote quizploegen.
Op hoeveel manieren kan dit als:

• Jan en Greet absoluut in dezelfde ploeg willen?

Opgave B.

• Bereken 6 -1 x 0 + 2 : 2

Los op met ontbinden in factoren:

• $4x^{2}-4x-3=0$

Gegeven een kegel. De diameter van het grondvlak is 12 en de hoogte is 8. In de kegel past precies een bol.

• Bereken exact de oppervlakte en de inhoud van de kegel en de bol.

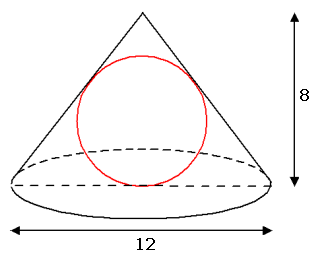
Opgave E.

Hier zie je aantal verschillende soorten verpakkingen. Zoek op Internet naar een formule voor de effectiviteit van verpakkingen. Bepaal van minimaal 5 verschillende soorten verpakkingen wat de 'effectiviteit' is.

De wortelfunctie $f$ heeft als startpunt $(-2,-2)$ en gaat door het punt $(6,6)$.

• Stel een functievoorschrift op voor de functie $f$.

Opgave G.

Gegeven $f(x)= \ln(x^2-6x) - \ln(x)$

• Bepaal de afgeleide

Opgave H.

Gegeven is de parabool $y^2-4y-6x-20=0$

• Geef het brandpunt en de richtlijn en schets de parabool.

Opgave I.

We nemen 5 letters A, B, C, D en E. We gaan hiermee 'woorden' maken. Letters mogen meerdere keren gebruikt worden. Er zijn echter wel een aantal beperkingen:

• Naast een A mag een B of E staan.
• Naast een B mag een A, C, D of E staan.
• Naast een C mag een B of D staan.
• Naast een D mag een B, C of E staan.
• Naast een E mag een A, B of D staan.

1. We gaan eerst kijken naar woorden van 2 letters.
   Waarom is AA geen goed woord?
   Hoeveel verschillende woorden van 2 letters kun je maken?
2. We kijken naar woorden van 3 letters.
   Is het woord EDE een goed woord?
   Is BED een goed woord?
   Hoeveel woorden van 3 letters kun je maken die beginnen met A?
   Hoeveel woorden van 3 letters kun je maken?
3. We kijken naar woorden van 4 letters.
   Hoeveel woorden van 4 letters kun je maken met als eerste en laatste letter een C?
   Hoeveel woorden van 4 letters kun je maken?
4. We kijken naar woorden van 5 letters.
   Hoeveel woorden van 5 letters kan je maken die met dezelfde letter beginnen en eindigen?

Jan en Piet willen elkaar morgen tussen 11.00 en 12.00 uur treffen op het station. Ze spreken af dat ze een kwartier op elkaar zullen wachten en dan weer vertrekken.

• Hoe groot is de kans dat ze elkaar treffen?

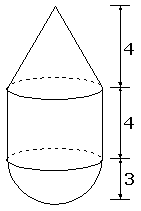
Dit object bestaat uit een kegel, cilinder en een halve bol.

• Bereken de oppervlakte op 1 decimaal nauwkeurig.

Opgave L.

Iemand heeft een rechthoekig stuk zink, 80 cm breed. Hij wil daarvan een goot maken met rechthoekige doorsnede.

• Ga na, wanneer de goot een zo groot mogelijke doorsnede heeft.

Opgave M.

Toon aan:

$
\left( {\begin{array}{*{20}c}
   {n + 2}  \\
   k  \\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
   n  \\
   k  \\
\end{array}} \right) + 2 \cdot \left( {\begin{array}{*{20}c}
   n  \\
   {k - 1}  \\
\end{array}} \right) + \left( {\begin{array}{*{20}c}
   n  \\
   {k - 2}  \\
\end{array}} \right)
$

Opgave N.

Nora vertrekt om 8 uur en legt gemiddeld 12 km/uur af. Hans vertrekt om 10 uur en fietst Nora achterna met een gemiddelde snelheid van 18 km/uur.

• Hoe laat zullen ze elkaar ontmoeten?

• Hoe begin ik aan zo'n vergelijking?

Ik weet de keuze van mijn onbekende zelfs niet...

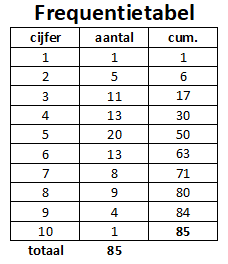
Opgave O.

Gegeven een frequentietabel met 85 waarden.

• Bereken de kwartielafstand.

Hoe kan je deze wortels in de standaardvorm zetten?

1. $
   \eqalign{\left( {\frac{{\sqrt 3 }}{2}} \right)^3}
   $
2. $\eqalign{
   \left( {\sqrt {\frac{4}
   {3}} } \right)^5
   }$
3. $\eqalign{
   \left( {\sqrt {\frac{3}
   {2}} } \right)^3
   }$
4. $\eqalign{
   \left( {\frac{{2\sqrt 3 }}
   {{\sqrt 2 }}} \right)^4
   }$

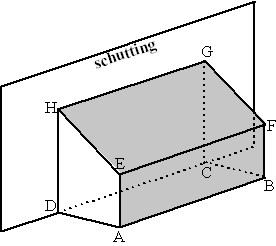Met behulp van een frame van uitschuifbare tentstokken AE en BF en een rechthoekig zeil van 5 bij 10 meter wordt tegen een schutting een opslagruimte gemaakt in de vorm van een recht prisma AEHD.BFGC.

De grensvlakken AEHD en BFGC blijven open en hebben elk de vorm van een trapezium met rechte hoeken in A, D, B en C.

De breedte AD van de opslagruimte is 3 meter. Het zeil wordt met de lange kant van 10 meter op de grond bevestigd langs AB.

Het zeil wordt over de stok EF strak gespannen naar de schutting waar het zo hoog mogelijk wordt bevestigd. In de figuur is dat langs HG.

De korte kant van het zeil valt langs AE en EH. AE + EH = 5 meter. Doordat AE (= BF) variabel is, zal de hoogte van HG ook variabel zijn. De inhoud V van het prisma AEHD.BFGC hangt af van de lengte h van AE.

• Geef een formule voor V met h in m en V in m³.

Opgave R.

In een vaas zitten 8 witte, 4 blauwe en 2 rode ballen. We trekken steeds drie ballen uit de vaas zonder terugleggen.

• Bereken de kans op 2 witte ballen.

Martin wil een groepsfoto maken van een groep van zeven personen. De personen staan willekeurig op een rij. Harry en Tjitske zijn groepsleden.

• Wat is de kans dat Harry en Tjitske naast elkaar op de foto staan?

EINDE