
$
\eqalign{
& \sin 38^\circ = \frac{{352}}
{{parcours}} \cr
& parcours = \frac{{352}}
{{\sin 38^\circ }} \approx 572\,\,meter \cr}
$
OPGAVE 2
$
\eqalign{
& \tan \angle BAC = \frac{3}
{7} \Rightarrow \angle BAC \approx 23,20^\circ \cr
& \cos \angle CAE = \frac{5}
{6} \Rightarrow \angle CAE \approx 33,56^\circ \cr
& \angle BAE \approx 56,8^\circ \cr}
$

OPGAVE 5
$
\eqalign{
& \sin 10^\circ = \frac{{h_A }}
{{5000}} \Rightarrow h_A \approx 868,2\,\,meter \cr
& \cos 10^\circ = \frac{{v_A }}
{{5000}} \Rightarrow v_A \approx 4924,0\,\,meter \cr
& \tan 6^\circ = \frac{{h_M }}
{{6076,0}} \Rightarrow h_M \approx 638,6\,\,meter \cr
& h_{A + M} \approx 868,2 + 638,6 \approx 1506,8\,\,meter \cr}
$
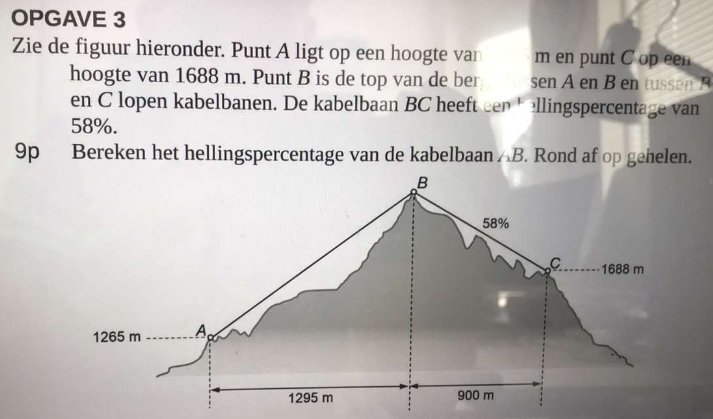
OPGAVE 3
$
\eqalign{
& \tan \angle C = \frac{{hoogte_{BC} }}
{{900}} = 0,58 \Rightarrow hoogte_{BC} = 522\,\,meter \cr
& hoogte_{AC} = (1688 - 1265) + 522 = 945\,\,meter \cr
& hellingspercentage_{AB} = \frac{{945}}
{{1296}} \times 100\% \approx 73\% \cr}
$

OPGAVE 4
$
\eqalign{
& \tan 13,6^\circ = \frac{{17}}
{{rhz_1 }} \Rightarrow rhz_1 \approx 70,3\,\,meter \cr
& lengte \approx 105\,\,meter \cr
& \tan \left( {49,7 - 13,6} \right) = \frac{{rhz_2 }}
{{70,3}} \Rightarrow rhz_2 = 51,3\,\,meter \cr
& breedte \approx 68\,\,meter \cr}
$