Alles op een rijtje?

In de wiskunde kom je nog wel 's rijtjes getallen tegen. Bij testen en quizzen trouwens ook. Vaak moet je die rijtjes dan voortzetten. Je weet wel: wat is het volgende getal?

Bij deze opdracht hoort een werkblad:

• Werkblad alles op een rijtje

Geef de volgende term:

1. 1, 2, 4, 8, 16, ...
2. 1, 1, 2, 3, 5, 8, 13, 21, ...
3. 1, 9, 2, 8, 3, 7, 4, 6, 5, ...
4. 1, 11, 121, 1331, 14641, ...
5. 1, 121, 12321, 1234321, 123454321, 12345654321, 1234567654321, 123456787654321, 12345678987654321, ...
6. 1, 10, 11, 100, 101, 110, ...
7. o, t, t, f, f, s, s, e, n, t, e, t, t, f, f, s, s, e, n, t, t, t, t, t, ...
8. 0, 5, 8, 12, 20, 50, ...
9. 30, 105, 385, 1001, 2431, ...
10. 1, 11, 21, 1211, 111221, 312211, ...
11. $\frac{1}{2}$, $\frac{3}{4}$, hv, hv, $\frac{1}{2}$, $\frac{3}{4}$, hv, ... 

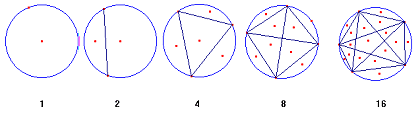
Kijken we nog even naar het volgende rijtje:

1, 2, 4, 8, 16, ...

Voorbeeld:

• Neem een aantal punten op een cirkel en teken alle verbindingskoorden; het aantal gebieden waarin de cirkelschijf door de koorden wordt verdeeld hangt uiteraard af van het aantal punten (zeg n).

• Op het werkblad staat een figuur met 6 punten. Tel het aantal gebieden. Wat valt je op?
  Zie Werkblad alles op een rijtje

Opdracht 3

Driehoeksgetallen zijn het eenvoudigste voorbeeld van veelhoekgetallen. Veelhoekgetallen werden door de Grieken al bestudeerd. Ze kunnen als stippenpatronen worden weergegeven. Hieronder zie je het stippenpatroon van de driehoeksgetallen.

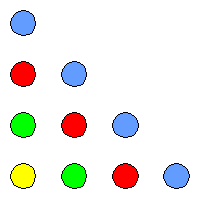
De rij van driehoeksgetallen begint zo: 1, 3, 6, 10, 15, 21, 28, ...

• Geef een formule voor het n-de getal in deze rij. 

In deze laatste opdracht kijken we naar het aantal diagonalen van een n-hoek

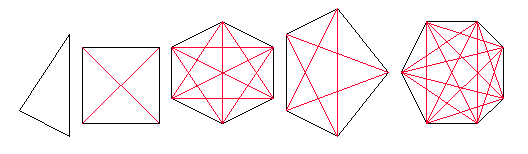
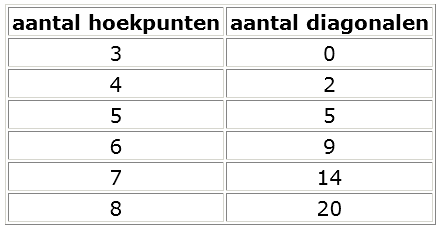
Het is niet moeilijk te "voorspellen" hoeveel diagonalen een 9-hoek of een 10-hoek heeft...

1. Hoeveel diagonalen heeft een 12-hoek?
2. Hoeveel diagonalen heeft een 50-hoek?
3. En een 1000-hoek?
4. Geef een formule voor het aantal diagonalen van een n-hoek.

Zet je antwoorden in een worddocument en zet dat in je map.