3. Als je een konijn vraagt...

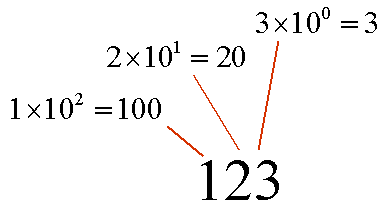
Een gedicht over hoe konijnen rekenen:

Als je een konijn vraagt
Hoeveel is twee keer twee,
Dan is het antwoord tien;
En twee keer drie is twaalf,
En drie keer drie is eenentwintig.
Want het konijnenstelsel is viertallig,
Dat staat in verband met de constante
Hoeveelheid poten per konijn,
En ook per poot het aantal tenen.
Toch zijn konijnen
In rekenen niet altijd meesters;
Hun optellen lijkt nergens naar,
Hun staartdelingen schieten te kort,
Breuken, daar maken ze niets van.
Maar vermenigvuldigen, daar zijn ze goed in,
En ze weten ook goed raad met wortels:
Het aantal oren, tel ze maar,
Is de wortel uit het aantal poten.

RUDY KOUSBROEK

Dit gedicht gaat over rekenen. Hoe konijnen optellen, vermenigvuldigen, delen en worteltrekken. Maar 2×2=10? En 2×3=12? 3×3=21? Klopt dat wel? Kunnen konijnen wel rekenen? Slaat het nu ergens op? Of is het onzin? In het gedicht staat 'het konijnenstelsel is viertallig', maar wat betekent dat precies?

Het tientallig stelsel

Wij rekenen in het tientallig stelsel. Ons getallenstelsel is een positiesysteem. De waarde van een cijfer hangt af van de positie in het getal. Bij 123 stelt de '3' drie eenheden voor, de '2' stelt twee tientallen voor en de '1' is een hondertal. Elke positie van een getal stelt een macht van 10 voor.

$123=1·10^{2}+2·10^{1}+3·10^{0}$

Met de cijfers 0 ^t/_m 9 kan je allerlei getallen maken, je kunt er mee rekenen, tafels uit je hoofd leren, aftrekken, vermenigvuldigen, delen, machtsverheffen, worteltrekken.. en nog veel meer.

Dat is een veel handiger systeem dan bijvoorbeeld de romeinse cijfers.

Tellen

Je begint te tellen met 1. Dan komt 2, 3, 4,.. tot 9. Dan ga je over op de tientallen. Die '10' van ons wil dus zeggen '1' tiental en '0' eenheden. Je kunt daarmee doorgaan tot 99. Dan ga je over op de honderdtallen. Onze '100' is dus '1' honderdtal, '0' tientallen en '0' eenheden.

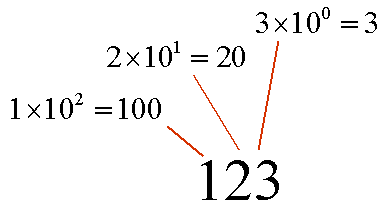
Het viertallig stelsel

Maar hoe zit dat dan in het viertallig stelsel? Hieronder zie je de getallen in het tientallig stelsel (links) met hetzelfde 'aantal' in het viertallig stelsel (rechts):

1$\to$1
2$\to$2
3$\to$3
4$\to$10
5$\to$11
6$\to$12
7$\to$13
8$\to$20
9$\to$21
10$\to$22
11$\to$23

12$\to$30
13$\to$31
14$\to$32
15$\to$33
16$\to$100
17$\to$101
18$\to$102
19$\to$103
20$\to$110
21$\to$111
22$\to$112

Bij het viertallig stelsel heb je alleen de cijfers 0, 1, 2 en 3. In het viertallig stelsel schrijf je onze '4' als '10'. In het viertalig stelsel komt '23' overeen met 2×4+3=11 in het tientallig stelsel.

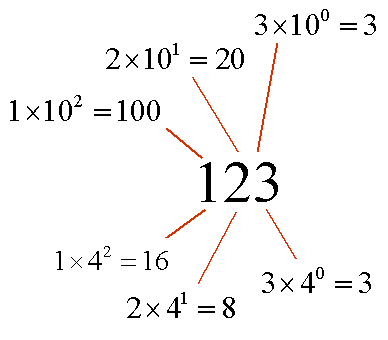
123 is in het viertallig stelsel gelijk aan 1·16+2·4+3=27 in het tientallig stelsel.

Controleer de rekenmethode van de konijnen in het gedicht hierboven. Klopt het allemaal?
Schrijf je antwoorden in het tekstvlak hieronder.

Opdracht

Hoe schrijf je "het aantal oren is de wortel uit het aantal poten" in het viertallig stelsel?

Laat zien dat ? in het viertallig stelsel overeenkomt met ? in het tientallig stelsel.