9. De gulden snede
 De gulden snede is de verdeling van een lijnstuk in twee delen, waarvan het kleinste zich verhoudt tot het grootste als het grootste tot het geheel. Er wordt wel 's beweerd dat de gulden snede een belangrijke rol in de beeldende kunst en architectuur speelt als norm voor harmonisch aandoende verhoudingen.
De gulden snede is de verdeling van een lijnstuk in twee delen, waarvan het kleinste zich verhoudt tot het grootste als het grootste tot het geheel. Er wordt wel 's beweerd dat de gulden snede een belangrijke rol in de beeldende kunst en architectuur speelt als norm voor harmonisch aandoende verhoudingen.
Op deze website kan je er van alles over vinden.
De verhouding tussen het 'lange en korte stuk' wordt wel het gulden getal genoemd en aangeduid met de Griekse letter $\phi$. (uitgesproken als phi)
$\Large\phi=\frac{1+\sqrt{5}}{2}\approx1,618$
Er is een verband tussen $\phi$ en de rij van Fibonacci uit de vorige opdracht.
De quotiëntrij van Fibonacci
Een quotiëntrij kan je maken door steeds opeenvolgende termen door elkaar te delen. Bij de rij van Fibonacci ziet dat er dan zo uit:
$
\Large\frac{1}{1},\,\frac{2}{1},\,\frac{3}{2},\,\frac{5}{3},\,\frac{8}{5},\,\frac{{13}}{8},\,\frac{{21}}{{13}},\,...
$
De termen van deze quotiëntrij gaan steeds dichter bij $\phi$ te liggen. Verder in de rij krijg je een steeds betere benadering van $\phi$.
De rij van Fibonacci en de gulden snede hebben dus alles met elkaar te maken.
De gulden rechthoek
Een rechthoek waarbij de lengte en breedte zich verhouden als $\phi$ staat tot $1$ wordt wel de gulden rechthoek genoemd. Hieronder zie je daarvan de constructie.
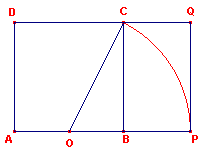
Met de constructie erbij: begin met een vierkant ABCD en kies het midden O van AB als middelpunt van een cirkel met straal OC...
AP en AD verhouding zich dan volgens de gulden snede.
|
In schilderijen kan je op verschillende manieren de gulden snede terug vinden.

Op het geheim van de gulden snede kan je nog veel meer vinden over de gulden snede. Niet verder vertellen...
|
Opdracht 1 |
Los de vergelijking $x^{2}-x-1=0$ op.
-
Gebruik (eventueel) je grafische rekenmachine.
Zie F2: Polynominal of F3: Solver.
-
Eén van de oplossingen is een bekend getal. Welk getal is dat?
|
|
Opdracht 2 |
Type in het rekenscherm van je grafische rekenmachine een willekeurig getal in en klik op EXE. Type 1+1$\div
$Ans in en klik een aantal keren op EXE. Ga hier mee door tot het getal op je scherm niet meer verandert.

Geef dat getal afgerond op 6 decimalen. Hoe heet het getal waar dit een benadering van is?
Zet je antwoord in het tekstvlak hieronder.
|
|
Opdracht 3 |
Hieronder zie je een schilderij van Hans Baggen. De schilder heeft als uitgangspunt de gulden snede genomen.

De lijnstukken AB en AE verhouden zich al de gulden snede en de lijstukken CD en DE verhouding zich ook als de gulden snede. Neem 's aan dat AE gelijk is aan $1$ meter.
-
Bereken de lengte van AB in cm nauwkeurig.
Zet je antwoord in het tekstvlak hieronder.
|
 De gulden snede is de verdeling van een lijnstuk in twee delen, waarvan het kleinste zich verhoudt tot het grootste als het grootste tot het geheel. Er wordt wel 's beweerd dat de gulden snede een belangrijke rol in de beeldende kunst en architectuur speelt als norm voor harmonisch aandoende verhoudingen.
De gulden snede is de verdeling van een lijnstuk in twee delen, waarvan het kleinste zich verhoudt tot het grootste als het grootste tot het geheel. Er wordt wel 's beweerd dat de gulden snede een belangrijke rol in de beeldende kunst en architectuur speelt als norm voor harmonisch aandoende verhoudingen.



