A. Konijnen en groeimodellen

In de wiskunde kan je verschillende groeimodellen tegen komen. In dit hoofdstuk bespreken we een aantal van die groeimodellen. Je zult tabellen tegen komen, formules en de bijbehorende grafieken.

Wortels

"Op een stuk landbouwgrond staan 24 wortels. Elke dag poot je daar 4 wortels bij. Hoeveel wortels heb je dan na 30 dagen?"

Er komen in 30 dagen 30·4=120 wortels bij. Ik had er al 24 dus in totaal heb je dan 144 wortels.

Neem het aantal wortels $N$ en de tijd $t$ in dagen. Je kunt dan de volgende formule opstellen:

$N = 4·t + 24$

Als je $t$ weet (bijvoorbeeld $t=30$) dan kan je met de formule $N$ uitrekenen:

$N = 4·30 + 24 = 120 + 24 = 144$

Dit noemen we lineaire groei:
$N = a·t + b$
$N$ is het aantal, $a$ is de toename per tijdseenheid, $t$ is de tijd en $b$ is de beginwaarde.

De groei is constant.

Cellen

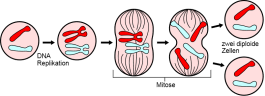Je hebt een cel en na een uur deelt de cel zich in tweeën. Na een uur splitsen deze twee cellen zich ook weer in tweeën. Enz.

Je krijgt dan 1, 2, 4, 8, 16, 32, ... Elk uur wordt het aantal vermenigvuldigd met hetzelfde getal. We noemen dat de groeifactor.

Al je dat in een tabel zet dan krijg je de volgende tabel:

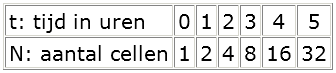
Met $t$ is de tijd in minuten en $N$ is het aantal cellen. Na 4 uur heb je 16 cellen of anders gezegd: $N=16$ op $t=4$.

Je kunt hierbij de volgende formule opstellen:
$N = 2^{t}$
Hierin is $N$ het aantal cellen en $t$ is de tijd in uren.
Na 10 uur heb je $N = 2^{10} = 1024$ cellen.

Dit noemen we exponentiële groei:
$N = b\cdot g^{t}$
$N$ is het aantal, $b$ is de beginwaarde, $g$ is de groeifactor en $t$ is de tijd.

De groei is afhankelijk van $N$.

Konijnen

Als er genoeg voedsel is neemt het aantal konijnen in een gebied aanvankelijk exponentiëel toe. Als er te veel konijnen komen neemt de de groei af wegens voedselgebrek. Er zit een bovengrens aan het aantal konijnen dat het gebied kan bevatten. Dit soort groei heet logistische groei.

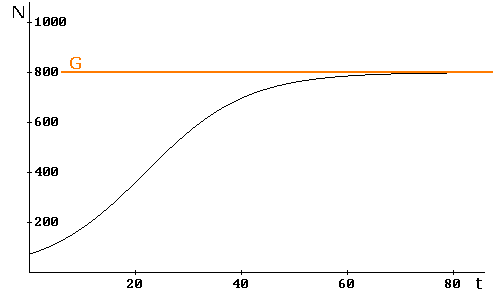
Hierboven zie je een voorbeeld van logistische groei. De grafiek heeft een soort S-vorm. De bijbehorende formule is:

$N = \Large\frac{800}{1+10·0,9^{t}}$

De grenswaarde $G$ is 800, g is 0,9 en b is gelijk aan 10. Dat lijkt op beginwaarde en groeifactor, maar dat is toch een beetje anders.

Logistische groei
$N = \Large\frac{G}{1+b·g^{t}}$
$N$ is het aantal, $G$ is de grenswaarde, $b$ de beginwaarde, $g$ is de groeifactor en $t$ is de tijd.

De groei is afhankelijk van $N$ en $G$.

Opdracht 1

Dit is een voorbeeld van lineaire groei:

Geef de formule.

Opdracht 2

Je zet €? op een spaarrekening. Je krijgt 5% rente per jaar. De rente wordt jaarlijks bijgeschreven op je rekening.

Hoeveel spaartegoed heb je na 10 jaar?
(rond af op hele euro's)

TIP: dit is een voorbeeld van exponentiële groei. Stel eerst de bijbehorende formule op. Wat is de 'beginwaarde'? Wat is de 'groeifactor?

TIP: de groeifactor is 1,05

Opdracht 3

Hier staat een grafiek van een exponentiëel verband.

Je wilt laten zien dat de formule $N=10·1,25^{t}$ klopt. Leg uit waar die $10$ vandaan komt? Hoe bereken je die $1,25$?

exponentiële functies

Opdracht 4

Een forellenkwekerij heeft een vijver laten aanleggen. Hier worden op t=0 een aantal forellen uitgezet. Er wordt verondersteld dat de groei logistisch zal zijn. Er geldt:

$N = \Large\frac{4800}{1+5·0,8^{t}}$

Met $N$ het aantal forellen op tijdstip $t$ in maanden.

Hoeveel forellen heeft men uitgezet?

Hoeveel forellen zijn er na 6 maanden?

Na hoeveel maanden zijn er ongeveer 4000 forellen?

Wat is het maximaal aantal forellen?

Wanneer is de groei maximaal?