voorkennis
Lijnstukken en wortels
In een vierkant met zijde $a$ is de lengte van een diagonaal gelijk aan $a\sqrt{2}$.
Voorbeeld

De lengte van $BE$ en $MN$ kun je snel zien. $NM$=$2\sqrt{2}$ en $BE$=$4\sqrt{2}$.
De zijde×hoogte-methode
De oppervlakte van een driehoek bereken je met
Opp($\Delta$)=$\frac{1}{2}$×zijde×hoogte
Maar dat kan op 3 manieren. Daarmee kan je soms 'handig' een onbekende zijde of onbekende hoogte berekenen.
Voorbeeld

- Bereken de lengte van $AM$
Antwoord
$BC=13$ (stelling van Pythagoras)
$5\cdot12=13\cdot AM$
$AM=4\frac{8}{13}$
De cosinusregel
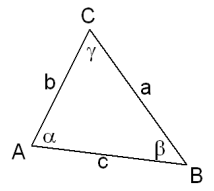
- $a^{2}=b^{2}+c^{2}-2bccos(\alpha)$
- $b^{2}=a^{2}+c^{2}-2accos(\beta)$
- $c^{2}=a^{2}+b^{2}-2abcos(\gamma)$
Hoeken in de ruimte
Voor het berekenen van hoeken in ruimtefiguren gebruik je het volgende werkschema:
- Werk in een geschikte driehoek of een geschikt diagonaalvlak
- Teken deze driehoek of dit diagonaalvlak apart
- Bereken de gevraagde hoek door een goniometrische verhouding te gebruiken. Bereken hiervoor zo nodig eerst nog een zijde.
Hoeken en vectoren
Voor de hoek tussen de vectoren $
\underline a
$ en $
\underline b
$ geldt:
$
\cos \left( {\angle \left( {\underline a ,\underline b } \right)} \right) = \frac{{\underline a \cdot \underline b }}{{\left| {\underline a } \right| \cdot \left| {\underline b } \right|}}
$
met $
\underline a \ne \underline 0
$ en $
\underline b \ne \underline 0
$
De hoek tussen twee lijnen
Als je de hoek wilt berekenen tussen de lijn $l$ en $k$ dan bereken je de hoek $\varphi$ tussen de richtingsvectoren van $l$ en $k$. Als de hoek stomp is dan neem je $180-\varphi$.
Voorbeeld
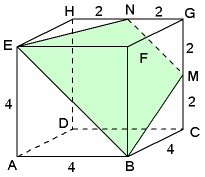
- Bereken $\angle ENM$
Zie uitwerking