Oplossing week 11
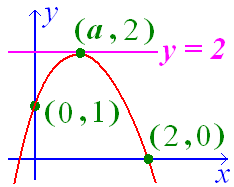
Boven zie je een parabool door de punten (0,1), (a,2) en (2,0).
- Bereken exact de waarde van a.
Oplossing
Gebruik de 'topformule'. In dit geval geldt:
$
y = p(x - a)^2 + 2
$
Invullen van (0,1) en (2,0) levert:
$
\begin{array}{l}
1 = p(0 - a)^2 + 2 \Rightarrow pa^2 = - 1 \Rightarrow p = - \frac{1}{{a^2 }} \\
0 = p(2 - a)^2 + 2 \Rightarrow p(2 - a)^2 = - 2\, \\
\end{array}
$
Vul de eerste in in de tweede:
$
\begin{array}{l}
- \frac{1}{{a^2 }}(2 - a)^2 = - 2 \\
\frac{1}{{a^2 }}(2 - a)^2 = 2 \\
(2 - a)^2 = 2a^{^2 } \\
4 - 4a + a^2 = 2a^2 \\
a^2 + 4a - 4 = 0 \\
\left( {a + 2} \right)^2 - 8 = 0 \\
a = - 2 \pm 2\sqrt 2 \\
\end{array}
$
Conclusie: $
a = - 2 + 2\sqrt 2
$
ps

$a=-2-2\sqrt{2}$ kan ook...