7. afstanden en vectoren
De afstand van een punt tot een vlak
De afstand van het punt $
P\left( {x_P ,y_P ,z_P } \right)
$ tot het vlak $
V:ax + by + cz = d
$ is:
$
d(P,V) =
$ $
\Large\frac{{\left| {ax_P + by_P + cz_P - d} \right|}}{{\sqrt {a^2 + b^2 + c^2 } }}
$
Voorbeeld 1
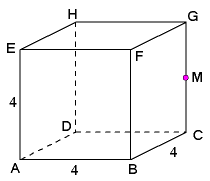
Gegeven is de kubus $ABCD.EFGH$ met ribbe 4. Het punt $M$ is het midden van $CG$.
- Bereken $d(F,BMH)$
De afstand van een punt tot een lijn
Het berekenen van de afstand van een punt $P$ tot een lijn $l$ met behulp van vectoren:
- Breng door $P$ het vlak $V$ aan dat loodrecht op $l$ staat.
- Bereken de coördinaten van het snijpunt $A$ van $V$ en $l$.
- Bereken $d(P,l)=PA$
Voorbeeld 2
Van driehoek $ABC$ is $A(-3,0,3)$, $B(3,1,-1)$ en $C(0,1,1)$.
- Bereken $d(A,BC)$
Voorbeeld 3
Teken een kubus ABCO·DEFG met de x as langs OA, de y as langs OC en de z as langs OG. De ribbe van de kubus is 2. Als P het midden is van ribbe FG en Q het midden van ribbe BC.
- Bereken dan de afstand van het punt P tot de lijn AQ.