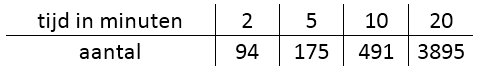
Onderzoek of hier sprake is van exponentiële groei.
Geef de groeifactor per minuut en de beginwaarde.

Om te laten zien dat het hier om exponentiële groei gaat moet je laten zien dat de groeifactor per minuut overal gelijk is. Hier is dat lastig omdat de 'stappen' van t niet overal hetzelfde zijn. Maar dat mag de pret niet drukken. Het gaat zo:

$
\eqalign{
& \left( {\frac{{175}}
{{94}}} \right)^{\LARGE \frac{1}
{3}} \approx 1,23 \cr
& \left( {\frac{{491}}
{{175}}} \right)^{\LARGE \frac{1}
{5}} \approx 1,24 \cr
& \left( {\frac{{3895}}
{{491}}} \right)^{\LARGE \frac{1}
{{10}}} \approx 1,23 \cr}
$

Je ziet de groeifactor is overal evengroot (ongeveer), dus kan je concluderen dat hier inderdaad sprake is van exponentiële groei.

• De groeifactor is (ongeveer) 1,23

Wat is nu de beginwaarde? Er geldt: $
94 = b \cdot 1,23^2 \Rightarrow b \approx 62
$

• De formule was N=62·1,23^t