4. lineaire vormen
Recht evenredig
$y$ is recht evenredig met $x$
- als je $x$ vermenigvuldigt met een getal dan moet je $y$ vermenigvuldigen met hetzelfde getal
- de formule heeft de vorm $y=ax$
- de tabel is een verhoudingstabel
- de grafiek is een lijn door de oorsprong
Voorbeeld
De prijs van kaas is recht evenredig met het gewicht. Koop je twee keer zoveel kaas dan moet je ook twee maal zo veel betalen...
Lineaire vergelijken van twee variabelen
De algemene vorm van een lineaire vergelijking met twee variabelen $x$ en $y$ is:
$ax+by=c$
De grafiek is een rechte lijn.
Voorbeeld
De vergelijking $2x-3y=12$ is een voorbeeld van een lineaire vergelijking met twee variabelen. Het is handig om te kijken naar $x=0$ en $y=0$.
Als $x=0$ dan $y=-4$
Als $y=0$ dan $x=6$.
Je kent dan twee punten van de grafiek: (0,-4) en (6,0). Je kunt dat de grafiek tekenen.
- Ligt het punt $A(8,1)$ op de grafiek?
Het opstellen van een lineaire vergelijking
Bij een pretpark is de toegangsprijs voor een volwassene €17 en voor een kind €12. Op een dag is er €19200 aan entreegeld binnengekomen. Als $x$ het aantal volwassenen is en $y$ het aantal kinderen dan kan je de volgende vergelijking opstellen:
$17x+12y=19.200$
- Als je weet dat er bij elkaar 1400 volwassenen en kinderen waren kan je dan uitrekenen hoeveel kinderen daar bij waren?
Een variabele vrijmaken
Je kunt bij de vergelijking $2x-3y=12$ de richtingscoëfficiënt en het snijpunt met de $y$-as vinden door $y$ vrij te maken.
$2x-3y=12$
$-3x=-2x+12$
$3x=2x-12$
$y=\frac{2}{3}x-4$
De richtingscoëfficiënt is $\frac{2}{3}$ en het snijpunt met de $y$-as is $(0,-4)$
Opdracht 1
De bewoners van appartementencomplex 'De Menthenbergh' hebben te maken met gemeenschappelijke servicekosten. De afspraak is deze kosten evenredig te verdelen op basis van de vloeroppervlakte.
De famile De Jager heeft een appartement met een vloeroppervlakte van 84 m2. Ze betalen jaarlijks €1890 aan servicekosten.
- De familie Knollenveld betaalt per jaar €2700 aan service kosten. Hoeveel is de vloeroppervlakte van hun appartement?
- De familie Het Haasje heeft een vloeroppervlakte van 75 m2. Dat is 1,2% van de totale vloeroppervlakte van het complex. Bereken de jaarlijkse servicekosten van het gehele complex.
Opdracht 2
Teken in een assenstelsel de grafieken van:
$
\begin{array}{l}
a.\,\,\,3x + 4y = 24 \\
b.\,\,\,x - 3y = 9 \\
c.\,\,\,x - y = 1 \\
\end{array}
$
Opdracht 3
Op een camping wordt een barbeque gehouden. Kinderen betalen €6,- en volwassenen €8,-. In totaal brengt de barbeque €1764,- op. Aan de barbeque doen 250 mensen mee.
- Bereken hoeveel kinderen er aan de barbeque meedoen.
Opdracht 4
Maak steeds $y$ vrij bij de volgende formules:
$
\begin{array}{l}
a.\,\,\,3x + 4y = 24 \\
b.\,\,\,x - 3y = 9 \\
c.\,\,\,x - y = 1 \\
\end{array}
$
Opdracht 1 uitwerking
Neem $y$ voor de servicekosten en $x$ voor de vloeroppervlakte. Er geldt:
$y=22,5\cdot x$
- Nu moet $2700=22,5x$. Dan is $x=120$. De vloeroppervlakte van de familie Knollenveld is $120$ m2.
-
De totale vloeroppervlakte van het complex is gelijk aan $6.250$ m2 (ga na!).
Dat is $22,5·6.259=140.625$ euro aan totale servicekosten.
Opdracht 2 uitwerking
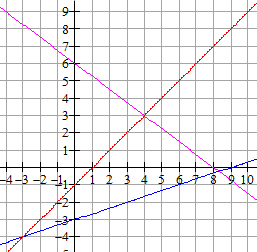
Opdracht 3 uitwerking
Neem $x$ voor het aantal kinderen en neem $y$ voor het aantal volwassenen. Er zijn dan twee vergelijkingen op te stellen:
$x+y=250$
$6x+8y=1764$
Neem $y=250-x$ en vul dat in de tweede vergelijking in. Je krijgt dan:
$6x+8(250-x)=1764$
$6x+2000-8x=1764$
$-2x=-236$
$x=118$
Er waren $118$ kinderen op de barbeque.
Opdracht 4 uitwerking
a.
$
\begin{array}{l}
3x + 4y = 24 \\
4y = - 3x + 24 \\
y = - \frac{3}{4}x + 6 \\
\end{array}
$
b.
$
\begin{array}{l}
x - 3y = 9 \\
- 3y = - x + 9 \\
3y = x - 9 \\
y = \frac{1}{3}x - 3 \\
\end{array}
$
c.
$
\begin{array}{l}
x - y = 1 \\
- y = - x + 1 \\
y = x - 1 \\
\end{array}
$
