0. voorkennis
Sinus, cosinus en tangens
$
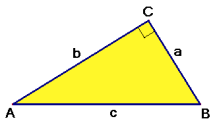
\eqalign{
& \sin \angle B = \frac{b}
{c} \cr
& \cos \angle B = \frac{a}
{c} \cr
& \tan \angle B = \frac{b}
{a} \cr}
$
Afspraak
Bij het berekenen van een hoek geef je het antwoord in één decimaal nauwkeurig, tenzij iets anders gevraagd wordt.
De sinusregel
In elke driehoek $ABC$ geldt de sinusregel:
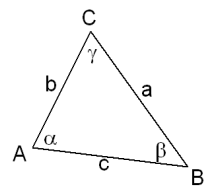
$\eqalign{\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}}$
De cosinusregel
In elke driehoek $ABC$ geldt de cosinusregel:
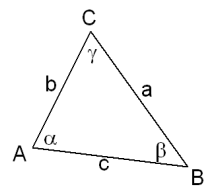
$a^2=b^2+c^2-2bc·\cos(\alpha)$
$b^2=a^2+c^2-2ac·\cos(\beta)$
$c^2=a^2+b^2=2ab·\cos(\gamma)$
Gelijkvormige driehoeken
$
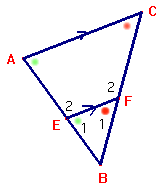
\Delta ABC \sim \Delta EBF
$
$
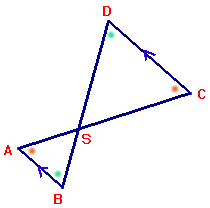
\Delta ABS \sim \Delta CDS
$
Je moet altijd toelichten waarom driehoeken gelijkvormig zijn. Je noteert daartoe de paren gelijke hoeken.
Zorg dat je bij de notatie van gelijkvormigheid de letters van de hoekpunten corresponderen met de overeenkomstige hoeken. Dat maakt het opstellen van de verhoudigstabel een stuk gemakkelijker.
Bijzonder rechthoekige driehoeken
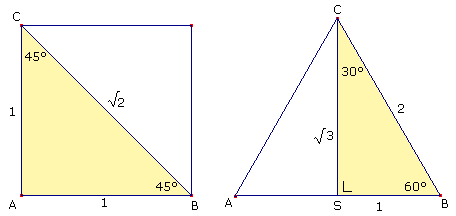
Er zijn twee verschillende tekendriehoeken: de 45°-45°-90°-driehoek en de 30°-60°-90°-driehoek.
Deze driehoeken kan je beschouwen als de helft van een vierkant resp. de helft van een gelijkzijdige driehoek. De zijden van deze driehoeken hebben bijzondere verhoudingen.
De hoek tussen twee lijnen
De richtingshoek van een lijn is de hoek die de lijn maakt met het positieve deel van de $x$-as.
Voor de richtingshoek $\alpha$ van de lijn $k$ geldt:
- $\tan\alpha=rc_k$
- $-90^\circ\lt\alpha\le90^\circ$
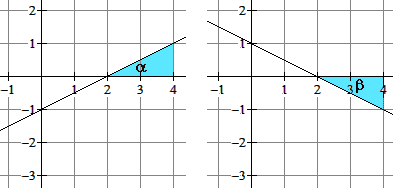
Voor de hoek $\varphi$ tussen twee lijnen met richtingshoeken $\alpha$ en $\beta$, waarbij $\alpha\gt\beta$, geldt:
- $\varphi=\alpha-\beta$ als $\alpha-\beta\le90^\circ$
- $\varphi=180^\circ-(\alpha-\beta)$ als $\alpha-\beta\gt90^\circ$