A. Twee telproblemen
Opgave 1
Twaalf vrienden trekken er een dagje op uit met de wagen. Er zijn 3 wagens beschikbaar.
- Op hoeveel manieren kan je drie groepjes van 4 maken?
Uitwerking
$
\eqalign{\frac{{\left( {\begin{array}{*{20}c}
{12} \\
4 \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
8 \\
4 \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
4 \\
4 \\
\end{array}} \right)}}{{3!}} = {\rm{5775}}}
$
Toelichting
Je kunt groep 1 op $
\left( {\begin{array}{*{20}c}
{12} \\
4 \\
\end{array}} \right)
$ manieren kiezen. Groep 2 kan je dan op $
\left( {\begin{array}{*{20}c}
8 \\
4 \\
\end{array}} \right)
$ manieren kiezen. De rest komt in groep 3 terecht. Dat kan op $
\left( {\begin{array}{*{20}c}
4 \\
4 \\
\end{array}} \right) = 1
$ manier.
Als de volgorde van de groepen van belang is dan kan je groep 1 t/m 3 op $
\left( {\begin{array}{*{20}c}
{12} \\
4 \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
8 \\
4 \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
4 \\
4 \\
\end{array}} \right)
$ manieren samenstellen, maar in dit geval is de volgorde van de groepen niet van belang. Je kunt derhalve de groepen 1, 2 en 3 onderling nog verwisselen. Je moet nog delen door $3!$
Begrip en inzicht
Als de volgorde van de groepen niet belangrijk is dan zijn de samenstelling van I. en II. in onderstaand plaatje identiek.
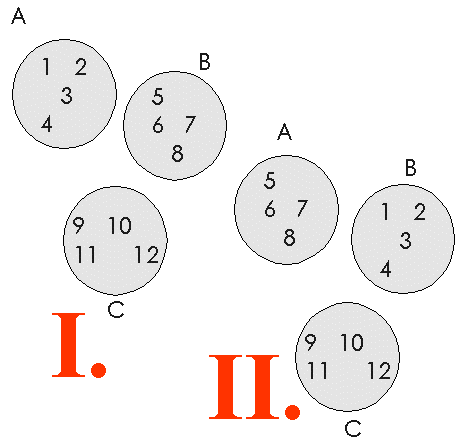
Ik heb ze echter in de berekening $
\left( {\begin{array}{*{20}c}
{12} \\
4 \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
8 \\
4 \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
4 \\
4 \\
\end{array}} \right)
$ wel allebei geteld.
Sterker nog: er zijn zelfs 6 verdelingen zoals I. en II. die we allemaal hebben meegeteld. Je moet dus nog delen door 6.
Opgave 2
Een groep van 24 studenten moet verdeeld worden in 3 even grote quizploegen.
Op hoeveel manieren kan dit als:
- Jan en Greet absoluut in dezelfde ploeg willen?
Uitwerking
-
$
\eqalign{\frac{{\left( {\begin{array}{*{20}c}
{22} \\
8 \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
{14} \\
8 \\
\end{array}} \right)}}{{3!}} = {\rm{160}}{\rm{.044}}{\rm{.885}}}
$
Toelichting
Er zijn hier verschillende mogelijkheden. Ik zou denken: ik zet die 2 even apart, maak 2 groepen van 8 en dan komen die 2 wel in de derde groep. Uiteraard kan je dan de groepen onderling weer verwisselen dus:
Het aantal manieren is $\eqalign{\frac{\pmatrix{22\\8}\cdot\pmatrix{14\\8}}{3!}}$
Maar voor hetzelfde geld kan je zeggen: ik stop die 2 in de eerste groep....
Het aantal manieren is $\eqalign{\frac{\pmatrix{22\\6}\cdot\pmatrix{16\\8}}{3!}}$
Of zelfs: ik stop ze in de tweede groep:
Het aantal manieren is $\eqalign{\frac{\pmatrix{22\\8}\cdot\pmatrix{14\\6}}{3!}}$
Het maakt allemaal niet uit...
Begrip en inzicht
- Voor de groepen waar Jan en Greet niet inzitten kan je kiezen uit 22 c.q. 14 studenten. Jan en Greet zitten dan in derde groep. Deze groepen kan onderling weer verwisselen zodat je uitkomt op het gegeven antwoord.