3. Machten en wortels
Het is werkelijk een wonder... eerst heb je optellen, 5+7=12, dat is mooi... dan 4+4+4+4+4, dat is dus 5 keer 4 is 20... vermenigvuldigen... dat is dus herhaald optellen! Dan krijg je 5·5·5·5, maar dat is dan 54, herhaald vermenigvuldigen... maar als je dan machten gaat vermenigvuldigen dan moet je de exponenten optellen...
53·55=58
Bent u daar nog? Zoals gezegd: machten en wortels zijn één pot nat... op je GR heb je een knopje voor machten: [^], maar er is ook een aparte functie voor kwadraat ([2]) en onder [MATH] zelfs een aparte functie voor de derdemacht ([3]).
In plaats van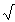 
3 kan je ook schrijven 
.
Ga maar na: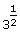 
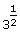·=31=3 dus... Op je GR heb je , 
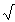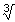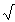en x (zie [MATH]), maar je kan dus ook werken met gebroken exponenten. Sterker nog: bij differentiëren maak je daar zelfs juist veel gebruik van...
Opgave 1
Bereken uit het hoofd en controleer je antwoord met je rekenmachine:
- 3-2=
- 50=
- 07=
- 00=
Opgave 2
Bereken op 2 decimalen nauwkeurig:
Opgave 3
Aanwijzingen: Het ! (=faculteit) kan je vinden onder [MATH] en dan kiezen voor PRB (probability=kansrekenen). De e (het grondtal van de natuurlijke logaritme) kan je vinden bij 
[¸] en bij [LN].
Bereken op 4 decimalen nauwkeurig:
