|
De formule $\eqalign{y=\frac{a}{x}}$
Als $x$ en $y$ omgekeerd evenredig zijn dan:
-
Als je $x$ vermenigvuldigt met $k$ dan deel je $y$ door k.
-
Het product $xy$ is constant, er geldt: $xy=a$
-
De formule heeft de vorm $\eqalign{y=\frac{a}{x}}$.
Grafiek
Meestal beperken we ons bij 'omgekeerd evenredig' tot positieve waarden van $x$ en $y$. Hieronder zie je de grafiek van de functie $\eqalign{y=\frac{12}{x}}$.
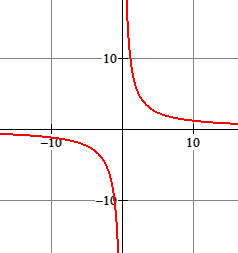
De grafiek bestaat uit twee 'takken' en wordt hyperbool genoemd.
|
Gebroken vergelijkingen oplossen
Een vergelijking zoals $\eqalign{\frac{5}{x+3}=\frac{2}{3}}$ heet een gebroken vergelijking. In een gebroken vergelijking komt de variabele $x$ in een noemer voor.
Voor het oplossen van gebroken vergelijkingen kun je kruislings vermenigvuldigen.
-
Uit $\eqalign{\frac{a}{b}=\frac{c}{d}}$ volgt $ad=bc$
Soms moet je als er links of rechts geen breuk staat er een breuk van maken met 'eenden'. Kwaak?
Voorbeelden
Los op:
-
$
\eqalign{{3 \over {x + 3}} = {1 \over x}}
$
-
$
\eqalign{{{x - 1} \over 3} = {5 \over {x + 1}}}
$
-
$
\eqalign{x + {3 \over {x - 1}} = 5}
$
Zie uitwerkingen
|