|
Vergelijkingen
Bij het oplossen van de vergelijking
$\eqalign{\frac{x}{3}=7}$
schrijf je eerst
$\eqalign{\frac{x}{3}=\frac{7}{1}}$
Je kunt dan kruislings vermenigvuldigen:
$1·x=3·7$, dus $x=21$.
Algemeen
-
$\eqalign{\frac{x}{a}=b}$ geeft $x=ab$
-
$\eqalign{\frac{a}{x}=b}$ geeft $x=\eqalign{\frac{a}{b}}$
Tip
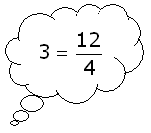 Als je dat lastig vindt dan kun je denken aan: Als je dat lastig vindt dan kun je denken aan:
$\eqalign{3=\frac{12}{4}}$
Wat moet je met $12$ en $3$ doen als je de $4$ niet weet? Enz....

|
Hellingsgetal berekenen
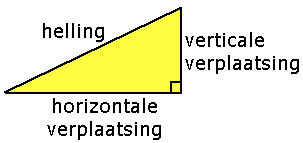
${\rm{hellingsgetal}}$ = $\Large\frac{{{\rm{verticale}}\,\,{\rm{verplaatsing}}}}{{{\rm{horizontale}}\,\,\,{\rm{verplaatsing}}}}$
In plaats van hellingsgetal=0,18 zeggen we ook wel hellingspercentage=18%.
Voorbeeld
Bij een helling met hellingsgetal 0,18 is de verticale verplaatsing 70 meter.
-
Bereken de horizontale verplaatsing
-
Bereken de lengte van de helling.
Uitwerking
$\eqalign{0,18=\frac{70}{horizontale\,verplaatsing}}$
$\eqalign{horizontale\,verplaatsing=\frac{70}{0,18}\approx389}\,meter$
$helling=\sqrt{70^2+389^2}\approx395\,meter$
|
|
De tangens van een hellingshoek
Bij een hellingshoek van $31^\circ$ hoort een hellingsgetal van $0,6$ of anders geformuleerd: de tangens van $31^\circ$ is 0,6 (afgerond op 1 decimaal) of ook:
Kortom: het hellingsgetal is de tangens van de hellingshoek.
Voorbeeld
Bij een helling is de verticale verplaatsing 30 meter en de horizontale verplaatsing 412 meter.
-
Bereken de tangens van de hellingshoek $\angle A$ op 3 decimalen nauwkeurig.
Uitwerking
-
$\tan(\angle A)=\frac{30}{412}\approx0,073$
Afspraak
-
Als er niet iets anders gevraagd wordt bereken je hoeken in één decimaal nauwkeurig.
Tip voor de rekenmachine
-
De meeste rekenmachines rekenen met drie verschillende hoekeenheden: DEG, RAD en GRAD.
-
Zorg ervoor dat je rekenmachiene op DEG (graden) is ingesteld.
-
DEG is een afkorting van degrees, het Engelse woord voor graden.

|
Van hellingsgetal naar hellingshoek
De vraag is nu: hoe kan je weten welk hellingsgetal er hoort bij welke hellingshoek en andersom?
Dezelf vraag: hoe kan je nu weten welke hoek er hoort bij een bepaalde waarde van de tangens en andersom?
Met je rekenmachine kan je bij een hoek de tangens vinden en bij een bepaalde waarde van de tangens welk hoek er bij hoort.
Voorbeeld
Er zit een knopje op de rekenmachine waar $tan$ op staat. Deze optie geeft je bij een hoek de waarde van tangens:
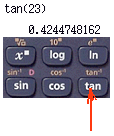
Bij een hoek van $23^\circ$ hoort een tangens van ongeveer $0,424$.
De optie boven het knopje voor de tangens heet $tan^{-1}$. Deze optie (de inverse tangens) geeft je bij een waarde voor de tangens de hoek.

Bij een tangens van $0,556$ hoort een hoek van ongeveer $29^\circ$
|