|
SOSCASTOA
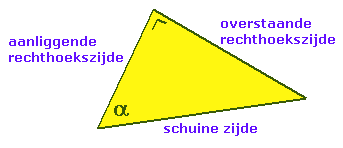
Sinus, cosinus en tangens worden goniometrische verhoudingen genoemd.
$
\eqalign{
& \sin \alpha = \frac{{{\text{overstaande rechthoekszijde}}}}
{{{\text{schuine zijde}}}} \cr
& \cos \alpha = \frac{{{\text{aanliggende rechthoekszijde}}}}
{{{\text{schuine zijde}}}} \cr
& \tan \alpha = \frac{{{\text{overstaande rechthoekszijde}}}}
{{{\text{aanliggende rechthoekszijde}}}} \cr}
$
Het woord goniometrie is afgeleid van het woord 'gonio' dat hoek betekent.

|
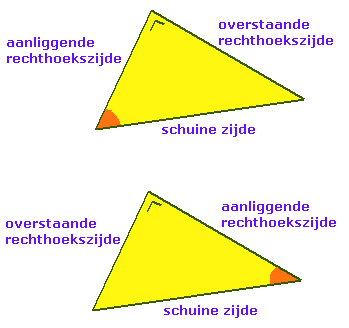
Zijden berekenen
In rechthoekige driehoeken kun je met behulp van sinus, cosinus en tangens zijden en hoeken berekenen.
Meer uitleg kan je vinden op:
|
|
Gelijkbenige driehoeken
Van een gelijkbenige driehoek waarvan de zijden gegeven zijn kun je de hoeken berekenen. Maar ook als je een hoek weet en een zijde...
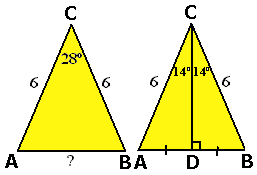
Uitwerking
Teken de lijn $CD$ loodrecht op AB.
Er geldt $AD=BD$.
$\sin(14^\circ)=\frac{AD}{6}$
$AD=6·\sin(14^\circ)\approx1,452$
$AB=2·AD\approx2,90$
|
Zelf rechte hoeken maken
Af en toe moet je eerst wat voorbereidend werk verrichten voordat je SOSCASTOA kunt toepassen. Dat is vooral zo als er geen driehoek met een rechte hoek is.
Voorbeeld
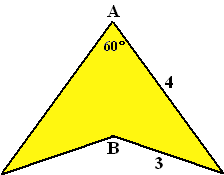
De pijlpunt is symmetrisch in lijn AB. De afmetingen zijn als in de figuur aangegeven.
Zie uitgewerkt
|