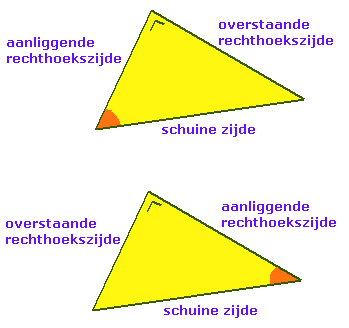
|
Het idee kijk uit de hoek die je weet of wilt weten is wel belangrijk. Het bepalen van de aanliggende c.q. overstaande rechthoekszijde hangt namelijk af van de hoek waar je het over hebt.
In een rechthoekige driehoek heb je altijd een schuine zijde (de zijde tegenover de rechte hoek) en twee rechthoekszijden (die vormen samen de rechte hoek). Als je vanuit een van de andere hoeken kijkt, dan heb je een rechthoekszijde die deel uitmaakt van die hoek, dat is de aanliggende rechthoekszijde. De andere rechthoekszijde ligt 'tegenover', aan de overkant! Dat is de overstaande rechthoekszijde.
Als je nu vanuit de andere hoek kijkt, dan is het verhaal precies hetzelfde, alleen dan is de overstaande rhz wat eerst de aanliggende rhz was... snap je?
Soms weet je van een rechthoekige driehoek twee zijden. Je kunt dan de derde zijde uitrekenen (met de stelling van Pythagoras) en je kunt de scherpe hoeken uitrekenen. Het hangt af welke zijden je kent of je dat met de sinus, cosinus of tangens doet.
Soms weet je van een rechthoekige driehoek een zijde en een hoek. De ander scherpe hoek kan je dan eenvoudig uitrekenen. Voor het berekenen van een zijde hangt er dan van af welke zijde je kent en welke zijde je wilt berekenen of je sinus, cosinus of tangens gebruikt.
Ik neem aan dat je dit 'ezelsbruggetje' kent: SOSCASTOA?
|
voorbeeld 1
 A ken ik en ik weet de SCHUINE zijde. Vanuit A gezien is BC de OVERSTAANDE rechthoekszijde. Een geval van SOS! Om BC te berekenen gebruik ik dus de SINUS:
$\eqalign{\sin 44°=\frac{BC}{58}}$
enz...
voorbeeld 2
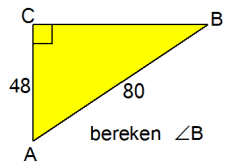
Vanuit B gezien ken ik de OVERSTAANDE rechthoekszijde en de SCHUINE zijde. Weer een geval van SOS. Om B te berekenen gebruik ik dus de SINUS.
$\eqalign{\sin\angle B=\frac{48}{80}}$
enz...
voorbeeld 3
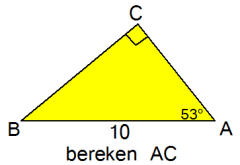
Ik ken A. Vanuit hoek A is AB de SCHUINE zijde en AC is de AANLIGGENDE rechthoekszijde. Een geval van CAS. Om AC te berekenen gebruik ik dus de cosinus.
$\eqalign{\cos 53°=\frac{AC}{10}}$
enz...
voorbeeld 4
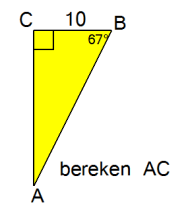
Ik ken hoek B, vanuit hoek B is BC de AANLIGGENDE rechthoekszijde en AC is de OVERSTAANDE rechthoekszijde. Een geval van TOA. Om AC te berekenen gebruik is dus de tangens.
$\eqalign{\tan 67°=\frac{AC}{10}}$
enz... |
