|
Het berekenen van BM.
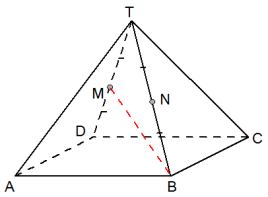
$AB=4$ en de hoogte is 4. Teken driehoek $DBT$ met het lijnstuk $BM$.
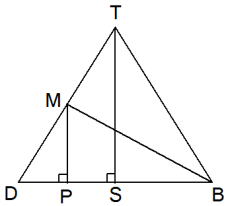
Teken $TS$ en $MP$ loodrecht op DB. $DB=4\sqrt{2}$. $\Delta DPM$ is de helft van $\Delta DST$. Dat betekent dan $PD=3\sqrt{2}$. $MP=2$ dus:
$BM=\sqrt{(3\sqrt{2})^2+2^2}=\sqrt{22}$
|
Het berekenen van CN.
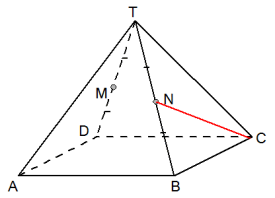
Teken $NQ$ loodrecht op $DB$ en $QR$ loodrecht op $BC$.
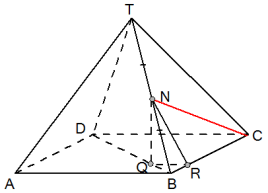
Je kunt de lengte van $CN$ berekenen in $\Delta RCN$. Omdat $QN=2$ en $QR=1$ moet $RN=\sqrt{5}$ zijn. Met $RC=3$ en de stelling van Pythagoras krijg je:
$CD=\sqrt{3^2+(\sqrt{5})^2}=\sqrt{14}$
|