|
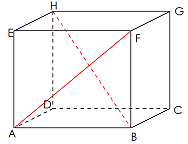Zijvlaksdiagonaal en lichaamsdiagonaal
 In de balk is $AF$ een zijvlaksdiagonaal en $BH$ een lichaamsdiagonaal.
Om de lengte van $AF$ of $BH$ te berekenen gebruik je de stelling van Pythagoras.
In een balk met ribben $a$, $b$ en $c$ is de lengte $L$ van een lichaamsdiaginaal:
$L=\sqrt{a^2+b^2+c^2}$
De lengte van een diagonaal van een vierkant met zijde $a$ is gelijk aan $a\sqrt{2}$.
|
Voorbeeld
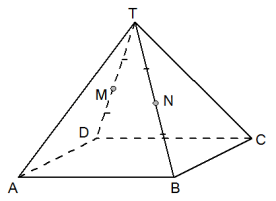
Gegeven is de regelmatige vierzijdige piramide T.ABCD met AB=4 en hoogte 4. Het punt M is het midden van DT en het punt N is het midden van BT.
Bereken exact:
-
BM
-
CN
Zie uitwerking
|
