|
Evenredig
$y$ is (recht) evenredig met $x$
-
vermenigvuldig je $x$ met een getal dan moet je $y$ met hetzelfde getal vermenigvuldigen
-
de bijbehorende tabel is een verhoudingstabel
-
de formule heeft de vorm $y=ax$
-
de grafiek is een rechte lijn door de oorsprong
|
Omgekeerd evenredig
$y$ is omgekeerd evenredig met $x$
-
vermenigvuldig je $x$ met een getal dan moet je $y$ door hetzelfde getal delen
-
het product $x·y$ is constant, dus $x·y=c$ ofwel $\eqalign{y=\frac{c}{x}}$
-
de grafiek is een hyperbool
|
|
Formule van de vorm $\eqalign{y=\frac{a}{x}+b}$
De grafiek van $\eqalign{y=\frac{a}{x}+b}$ met $a\gt0$ is voor $x\gt0$ afnemend dalend en heeft de lijn $y=b$ als grenswaarde.
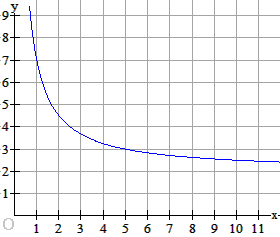
|
Voorbeeld
Gegeven $\eqalign{N = \frac{{50}}{t} + 15}$ met $t\gt0$
-
beredeneer wat de grenswaarde is
-
beredeneer hoe uit de formule van $N$ volgt dat de grafiek dalend is
-
vanaf welke $t$ is $N$ kleiner dan 18? Rond af op 1 decimaal
|