|
Een formule opstellen bij exponentiële groei
Is bij een exponentiële groei de hoeveelheid op twee tijdstippen bekend dan kun je de bijbehorende formule opstellen..
Je berekent eerst de groeifactor per tijdseenheid en daarna de beginhoeveelheid.
|
Voorbeeld 1
Gegeven is exponentiële groei met $N(4)=1040$ en $N(10)=2510$ met $t$ in dagen
Voorbeeld 2
Gegeven is exponentiële afname met $N(2)=800$ en $N(7)=200$ met $t$ in dagen.
|
|
Afspraak
Geef de beginhoeveelheid in dezelfde nauwkeurigheid als de gegevens, tenzij anders vermeld...
Zie de opmerking bij de uitwerkingen
|
Exponentiëel verband
Je kunt ook te maken met een exponentiëel verband waarbij tijd niet een van de variabele is. Je kunt dan niet spreken over de groeifactor per tijdseenheid, maar wel over de groeifactor per andersoortige eenheid.
|
|
Begrensde groei
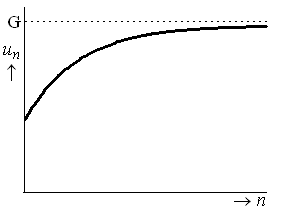
Hierboven zie je de grafiek van begrensde groei. Hierbij neemt de hoeveelheid in het begin toe maar bereikt uiteindelijk het verzadigingsniveau.
Voorbeeld 3
De formule $N=50(1-0,6^t)$ beschrijft een voorbeeld van begrensde groei.
-
Beredeneer dat het verzadigingsniveau gelijk aan 50 is.
|
Logistische groei
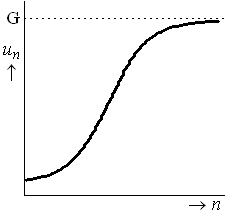
Hierboven zie je de grafiek van een ander groeiproces. In het begin neemt de hoeveelheid exponentieel toe, maar daarna wordt de groei afgeremd.
Voorbeeld 4
De formule $\eqalign{N=\frac{50}{1+18·0,6^t}}$ beschrijft een voorbeeld van logistische groei.
-
Beredeneer dat de grafiek stijgend is.
|








