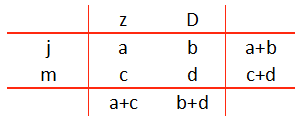|
Verschillen kwantificeren bij nominale variabelen
Voor het kwantificeren van een verschil bij een nominale variabele gebruiken we een associatiemaat.
-
Het percentageverschil (PV)
-
De odds-ratio (OR)
-
De phi-coëfficiënt (phi)
|
Vuistregels

De vuistregels worden gebruikt om te bepalen of het verschil groot, middelmatig of gering genoemd wordt.
|
|
Kruistabel
In de 2x2-kruistabel zijn de aantallen met de letters $a$, $b$, $c$ en $d$ aangegeven.
|
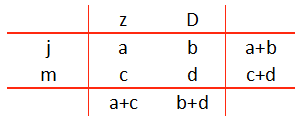 |
|
het percentageverschil PV
|
$$PV = \frac{a}{{a + b}} \times 100\% - \frac{c}{{c + d}} \times 100\% $$ |
|
de odds-ratio (OR)
|
$$OR = \frac{{\frac{a}{b}}}{{\frac{c}{d}}}\,\,ofwel\,\,OR = \frac{{ad}}{{bc}}$$ |
|
de phi-coëfficiënt (phi)
|
$$phi = \frac{{ad - bc}}{{\sqrt {\left( {a + b} \right)\left( {c + d} \right)\left( {a + c} \right)\left( {b + d} \right)} }}$$ |
|
Verschillen kwantificeren bij ordinale en kwantitatieve variabelen
Om bij een ordinale variabele het verschil te kwantificeren gebruik je het maximale verschil in cumulatief percentage. (max.Vcp)
Om bij een kwantitatieve variabele het verschil te kwantificeren gebruik je de effectgrootte . Je kunt ook de boxplots vergelijken.
De vuistregels staan op het formuleblad.
|
Het berekenen van max.Vcp
-
Bereken voor de variabele het cumulatieve percentage.
-
Bereken bij elke categorie het verschil van de cumulatieve percentages.
-
Kijk wat het grootste verschil is dat optreedt, dat is de max.Vcp
Zie bladzijde 66 voor een voorbeeld.
|
|
Het berekenen van de effectgrootte
Je kunt voor beide groepen het gemiddelde en de standaardafwijking berekenen. Je krijgt dan $\overline X_1$, $\overline X_2$, $S_1$ en $S_2$. De effectgrootte $E$ is dan gelijk aan:
$\eqalign{E = \frac{{\overline {{X_1}} - \overline {{X_2}} }}{{\frac{1}{2}\left( {{S_1} + {S_2}} \right)}}}$
Neem $\overline {{X_1}} > \overline {{X_2}} $ zodat de effectgrootte een positief getal oplevert.
|
Vuistregels bij effectgrootte

De vuistregels staan op het formuleblad.
|
|
Boxplots vergelijken
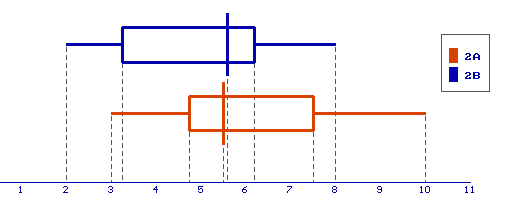
Om boxplots te vergelijken gebruiken we de vuistregels voor het vergelijken van boxplots...:-)
|
Vuistregels vergelijking van boxplots

De vuistregels staan op het formuleblad.
|
|
|
 formuleblad formuleblad |