3. afstanden in de ruimte
Afstand van punt tot lijn en van punt tot vlak
De afstand van een punt $P$ tot een lijn $l$ is de afstand van $P$ tot zijn loodrechte projectie $P'$ op $l$.
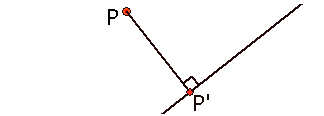
De afstand van een punt $P$ tot een vlak $V$ is de afstand van $P$ tot zijn loodrechte projectie $P'$ op $V$.
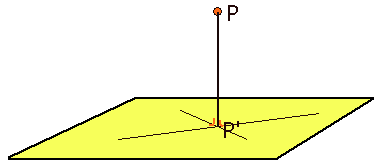
Afstanden bij evenwijdigheid
Voor het berekenen van afstanden bij evenwijdigheid kan je 't volgende overzicht gebruiken:
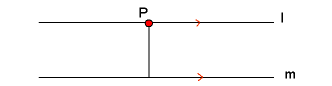
Bij $l\parallel m$ is $d(l,m)=d(P,m)$ met $P$ op $l$.
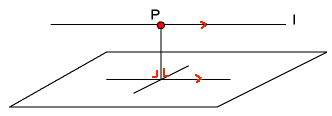
Bij $l\parallel V$ is $d(l,V)=d(P,V)$ met $P$ op $l$.
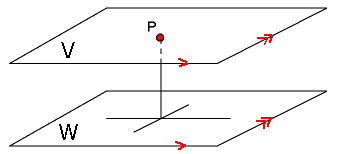
Bij $V\parallel W$ is $d(V,W)=d(P,W)$ met $P$ in $V$.
De afstand tussen twee kruisende lijnen
De afstand tussen de kruisende lijnen $l$ en $m$ is gelijk aan de afstand van $l$ tot het vlak evenwijdig aan met $l$, door $m$
Voorbeeld
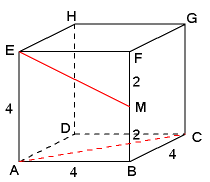
Gegeven is de kubus $ABCD.EFGH$ met ribbe $4$. Het punt $M$ is het midden van BF.
- Bereken $d(AC,EM)$
Uitwerking voorbeeld
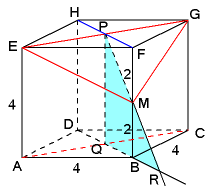
$d(AC,EM)=d(AC,EGM)=d(Q,EGM)=QS$
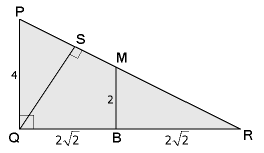
Zie uitwerkingenboek blz. 27