Omschrijven van aĚsin(x)+bĚcos(x)
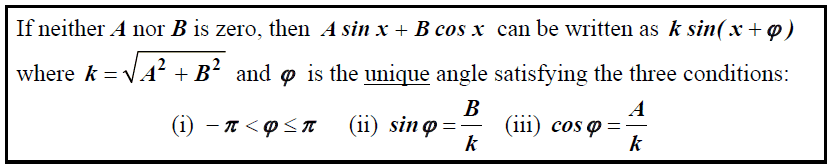
Voorbeeld 1
Naar aanleiding van Re: Variaties op goniometrie:
$
\eqalign{
& y = \sin (x) - \cos (x) \cr
& y \cdot \frac{1}
{2}\sqrt 2 = \sin (x)\frac{1}
{2}\sqrt 2 - \cos (x)\frac{1}
{2}\sqrt 2 \cr
& y \cdot \frac{1}
{2}\sqrt 2 = \sin (x)\frac{1}
{2}\sqrt 2 + \cos (x) \cdot - \frac{1}
{2}\sqrt 2 \cr
& y \cdot \frac{1}
{2}\sqrt 2 = \sin (x)\cos \left( {1\frac{3}
{4}\pi } \right) + \cos (x) \cdot \sin \left( {1\frac{3}
{4}\pi } \right) \cr
& y \cdot \frac{1}
{2}\sqrt 2 = \sin (x + 1\frac{3}
{4}\pi ) \cr
& y = \sqrt 2 \cdot \sin (x + 1\frac{3}
{4}\pi ) \cr}
$
Meer in 't algemeen kan dat ook zo:
$
\eqalign{
& y = \sin (x) - \cos (x) \cr
& A = 1\,\,en\,\,B = - 1 \cr
& k = \sqrt {1^2 + \left( { - 1} \right)^2 } = \sqrt 2 \cr
& - \pi \leq \varphi \leq \pi \,\,en\,\,\sin \varphi = \frac{{ - 1}}
{{\sqrt 2 }}\,\,en\,\,\cos \varphi = \frac{1}
{{\sqrt 2 }} \cr
& \varphi = - \frac{1}
{4}\pi \, \cr
& y = \sqrt 2 \cdot \sin \left( {x - \frac{1}
{4}\pi } \right) \cr}
$
Dat kan ook:-)
Voorbeeld 2
$
\eqalign{
& y = \sqrt 3 \sin (x) + \cos (x) \cr
& A = \sqrt 3 \,\,en\,\,B = 1 \cr
& k = \sqrt {\left( {\sqrt 3 } \right)^2 + 1^2 } = 2 \cr
& - \pi \leq \varphi \leq \pi \,\,en\,\,\sin \varphi = \frac{1}
{2}\,\,en\,\,\cos \varphi = \frac{{\sqrt 3 }}
{2} \cr
& \varphi = \frac{1}
{6}\pi \, \cr
& y = 2 \cdot \sin \left( {x + \frac{1}
{6}\pi } \right) \cr}
$