4. de ligging van een parabool ten opzichte van de x-as
Parabool en discriminant
Om de coördinaten van de snijpunten van de parabool $y=ax^2+bx+c$ met de $x$-as te berekenen los je de vergelijking $ax^2+bx+c=0$ op.
Het aantal oplossingen kan twee, één of nul zijn. Dat aantal hangt af van de discriminant:
$
D < 0
$
geen oplossing
geen snijpunten met de x-as
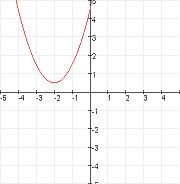
$
D = 0
$
één oplossing
één snijpunt met de x-as
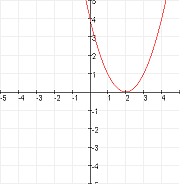
$
D > 0
$
twee oplossingen
twee snijpunten met de x-as
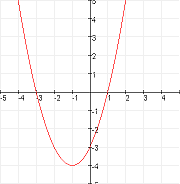
Functies met een parameter (B)
In $f(x)=x^2+4x+p$ heet $p$ een parameter. Een parameter is een hulpvariabele. Je hebt dan te maken met een 'familie van functies'. Voor elke waarde van $p$ een andere functie.
Voorbeeld
Gegeven $f(x)=2x^2-6x+p$. Voor welke waarde van $p$ raakt de grafiek van $f$ de $x$-as?
-
Bereken de snijpunten van $f$ met de $x$-as. Als $f$ raakt aan de $x$-as dan zou dat precies één snijpunt moeten opleveren,
$2x^2-6x+p=0$
$a=2$, $b=-6$ en $c=p$
$D=(-6)^2-4·2·p=36-8p$
Er geldt dat $D=0$
$36-8p=0$
$8p=36$
$p=4\frac{1}{2}$