2. differentiequotiŽnten en snelheden
Gemiddelde verandering
Er zijn twee manieren om over snelheid te praten:
- Gemiddelde snelheid over een periode
- snelheid op één moment
De gemiddelde snelheid bij een tijd-afstandgrafiek is $\eqalign{\frac{\Delta s}{\Delta t}}$
$\eqalign{\frac{\Delta N}{\Delta t}}$ is de gemiddelde verandering van $N$ per tijdseenheid.
Afspraak
Bij gemiddelde snelheden en gemiddelde verandering moet je de eenheid vermelden.
Voorbeeld
Een hardloper houdt onderweg zijn tussentijden bij:
Op het interval [0,10] geldt:
$\eqalign{\frac{\Delta s}{\Delta t}=\frac{3,5-0}{10-0}=0,35}$.
De gemiddelde snelheid op het interval [0,10] is 0,35 km/min.
Op het interval [10,15] geldt:
$\eqalign{\frac{\Delta s}{\Delta t}=\frac{5,5-3,5}{15-10}=0,40}$.
De gemiddelde snelheid op het interval [10,15] is 0,40 km/min.
Differentiequotiënt bij grafiek
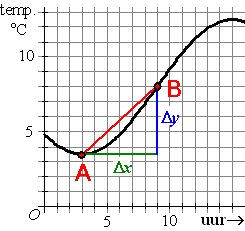
Het differentiequotiënt van y op $
\left[ {x_A ,x_B } \right]
$ is:
- de gemiddelde verandering van $y$ op $[x_A,x_B]$
- de richtingscoëfficiënt (ook wel helling) van de lijn $AB$
- $\Large \frac{{\Delta y}}{{\Delta x}} = \frac{{y_B - y_A }}{{x_B - x_A }}$
Voorbeeld
Gegeven:
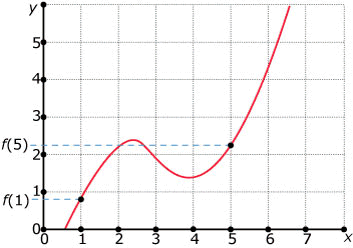
- Bereken de gemiddelde verandering op $[1,5]$
Antwoord
$
\eqalign{{{\Delta y} \over {\Delta x}} = {{f(5) - f(1)} \over {5 - 1}} = {{2,2 - 0,8} \over 4} = 0,35}
$
Differentiequotiënt bij formule
Het differentiequotiënt van $f(x)$ op het interval $[a,b]$ is gelijk aan:
$\eqalign{\frac{\Delta y}{\Delta x}=\frac{f(b)-f(a)}{b-a}}$
Voorbeeld
Gegeven $f(x)=x^2+5x$.
- Bereken het differentiequotiënt op $[-5,1]$
Antwoord
- $\eqalign{\frac{\Delta y}{\Delta x}=\frac{f(1)-f(-5)}{1--5}=\frac{6-0}{6}=1}$
Snelheid op één moment
Bij een tijd-afstandformule benader je de snelheid op een tijdstip $t=a$ met het differentiequotiënt op het interval $[a,a+\Delta t]$ met (bijvoorbeeld) $\Delta t=0,01$ of $\Delta t=0,001$
Voorbeeld
Gegeven is de formule $\eqalign{s=8-\frac{5}{t+2}}$. Hierin is $s$ de afgelegde weg in meter na $t$ seconden.
- Benader in m/s de snelheid op $t=1$ en op $t=2$. Neem beide keren $\Delta t=0,01$ en rond af op 2 decimalen.
Zie uitwerking