4. vergelijkingen in de meetkunde
Rekenregels voor wortels
Voor het vermenigvuldigen en delen van wortels gelden de volgende regels:
- $\sqrt{A}·\sqrt{B}=\sqrt{AB}$ voor $A\ge0$ en $B\ge0$
- $\eqalign{\frac{\sqrt{A}}{\sqrt{B}}=\sqrt{\frac{A}{B}}}$ voor $A\ge0$ en $B\gt0$
Rekenen met wortels
Je kunt bij $\sqrt{72}$ een factor voor het wortelteken brengen.
$\sqrt{72}=\sqrt{36·2}=\sqrt{36}·\sqrt{2}=6·\sqrt{2}$
Ga onder het wortelteken op zoek naar kwadraten. Neem een zo groot mogelijk kwadraat.
Afspraak
Breng een zo groot mogelijke factor voor het wortelteken en laat geen wortels in de noemer van een breuk staan.
Vergelijkingen met wortels
De vergelijking $x\sqrt{2}-3=\sqrt{6}$ is een voorbeeld van een lineaire vergelijking. Het oplossen komt neer op 'alle termen met $x$ naar links' en 'de rest naar rechts'. Soms kan je dan $x$ buiten haakjes halen.
Voorbeeld 1
$
\eqalign{
& x\sqrt 2 - 3 = \sqrt 6 \cr
& x\sqrt 2 = 3 + \sqrt 6 \cr
& x = {3 \over {\sqrt 2 }} + {{\sqrt 6 } \over {\sqrt 2 }} \cr
& x = {3 \over {\sqrt 2 }} \cdot {{\sqrt 2 } \over {\sqrt 2 }} + \sqrt 3 \cr
& x = {{3\sqrt 2 } \over 2} + \sqrt 3 \cr
& x = 1{1 \over 2}\sqrt 2 + \sqrt 3 \cr}
$
Voorbeeld 2
$
\eqalign{
& x\sqrt 2 + 2x = 8 \cr
& x\left( {\sqrt 2 + 2} \right) = 8 \cr
& x = {8 \over {\sqrt 2 + 2}} \cr}
$
Geheel tegen de afspraken in hoeft deze oplossing kennelijk niet verder herleid te worden. Maar 't is ook niet verboden...:-)
$
\eqalign{
& x = {8 \over {\sqrt 2 + 2}} \cr
& x = {8 \over {\sqrt 2 + 2}} \cdot {{\sqrt 2 - 2} \over {\sqrt 2 - 2}} \cr
& x = {{8\sqrt 2 - 16} \over {2 - 4}} \cr
& x = {{8\sqrt 2 - 16} \over { - 2}} \cr
& x = - 4\sqrt 2 + 8 \cr}
$
Bijzondere rechthoekige driehoeken
Er zijn twee verschillende tekendriehoeken: de 45°-45°-90°-driehoek en de 30°-60°-90°-driehoek.
Deze driehoeken kan je beschouwen als de helft van een vierkant resp. de helft van een gelijkzijdige driehoek. De zijden van deze driehoeken hebben bijzondere verhoudingen.
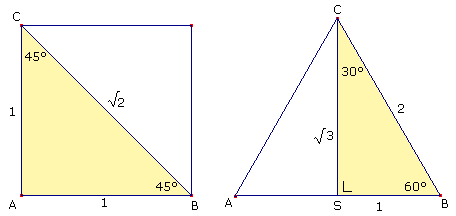
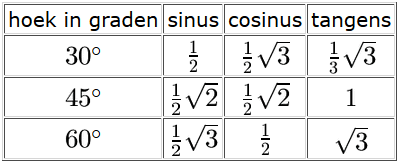
Met behulp van de driehoeken zijn de sinus, cosinus en de tangens van de hoeken 30°, 45° en 60° makkelijk te 'onthouden'.
Opdracht 1
-
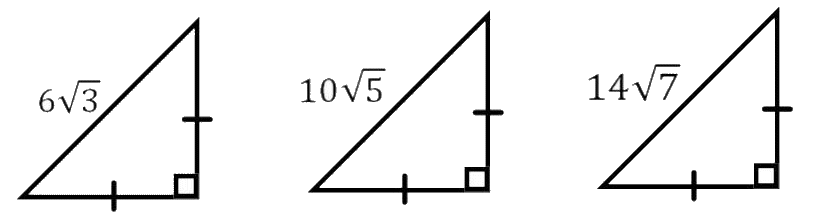
Bereken exact de lengte van de rechthoekszijden van bovenstaande driehoeken.
Wat valt je op?
Opdracht 2
-
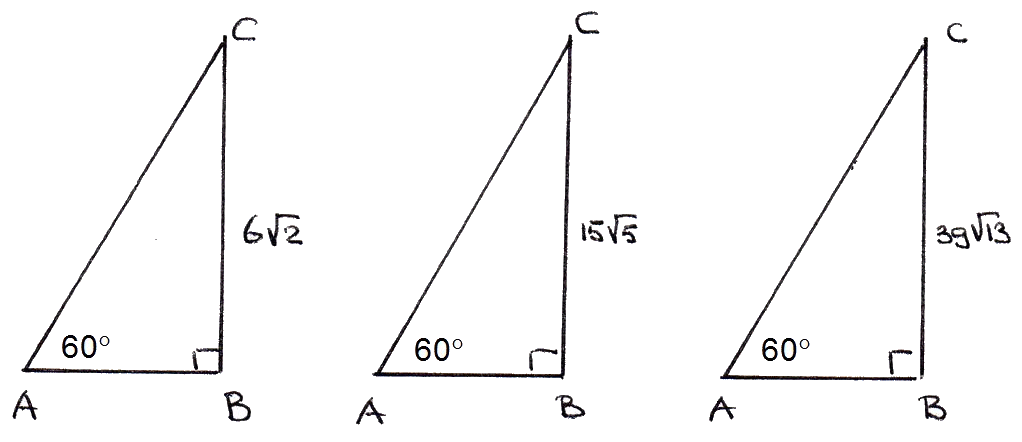
Bereken steeds exact de lengte van $AB$.
Wat valt je op?