3. ongelijkheden oplossen
Ongelijkheden algebraisch oplossen
Je kunt een ongelijkheid als $x^2\gt2x+3$ algebraisch oplossen door het linkerlid $f(x)$ te stellen en het rechterlid $g(x)$. Nadat je de vergelijking $f(x)=g(x)$ hebt algebraisch hebt opgelost en de grafieken van $f$ en $g$ hebt geschets lees je uit de figuur af waarde grafiek van $f$ boven de grafiek van $g$ ligt.
- Bij het oplossen van een ongelijkheid leer je het antwoord af op de $x$-as.
- Bij $f(x)\lt g(x)$ kijk je waar de grafiek van $f$ onder die van $g$ ligt.
- Bij $f(x)\gt g(x)$ kijk je waar de grafiek van $d$ boven die van $g$ ligt.
Werkschema het oplossen van de ongelijkheden $f(x)\lt g(x)$ en $f(x)\gt g(x)$
- Los de vergelijking $f(x)=g(x)$ op.
- Schets de grafieken van $f$ en $g$
- Lees uit de schets de oplossing af.
Voorbeeld
Los algebraisch op: $x^2\gt2x+3$
Uitwerking
$f(x)=x^2$ en $g(x)=2x+3$
$x^2=2x+3$
$x^2-2x-3=0$
$(x-3)(x+1)=0$
$x=3$ of $x=-1$
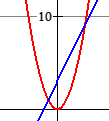
$x\lt-1$ of $x\gt3$
Vergelijkingen grafisch-numeriek oplossen
Het oplossen van een vergelijking met behulp van grafieken op de GR heet grafisch-numeriek oplossen. Je gebruikt daarbij de optie INTSECT bij G-Solv.
Werkschema grafisch-numeriek oplossen van vergelijkingen
- Voer het linkerlid van de vergelijking in bij Y1 en het rechterlid bij Y2.
- Noteer welke optie van de GR je gebruikt.
- Geef alle oplossingen in het gevraagde aantal decimalen of rond zelf verstandig af.
Bij bergelijkingen van de vorm $f(x)=0$ kan je ook gebruik maken van de optie ROOT.
Voorbeeld
Los op in 3 decimalen nauwkeurig: $x^3-8x=5-x^2$
Uitwerking
De oplossingen zijn $x\approx-3,074$ of $x\approx-0,607$ of $x\approx2,680$.
- Zie uitgewerkt met de GR.
Ongelijkheden numeriek-grafisch oplossen
Bij het oplossen van de ongelijkheid $f(x)\lt g(x)$ waarbij je niet algebraisch te werk hoeft te gaan mag je de vergelijking $f(x)=g(x)$ grafisch-numeriek oplossen.
Ga verder op dezelfde manier te werk als bij het algebraisch oplossen.