2. lengten en oppervlakten
Oppervlakte van vlakke figuren
Bij het berekenen van de oppervlakte van een vlakke figuur moet je de figuur soms opsplitsen in basisfiguren. Ook komt het voor dat je de figuur moet aanvullen tot een basisfiguur.
Formules voor de oppervlakte
$
\eqalign{
& O_{{\text{driehoek}}} = \frac{1}
{2} \cdot b \cdot h \cr
& O_{{\text{parallellogram}}} = b \cdot h \cr
& O_{{\text{trapezium}}} = \frac{1}
{2} \cdot \left( {a + b} \right) \cdot h \cr
& O_{{\text{cirkel}}} = \pi \cdot r^2 \cr}
$
Opgave 1
In een tuin is een zigzagpad aangelegd. De aanleg van het pad kost 80 euro per 10 m2.
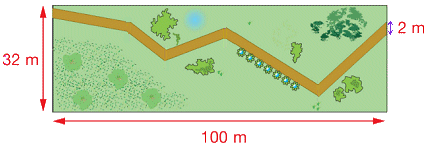
- Bereken de aanlegkosten van het pad.
Oppervlakte van regelmatige veelhoeken
Als van een driehoek twee zijden bekend zijn en de ingesloten hoek dan kan je de oppervlakte berekenen met:
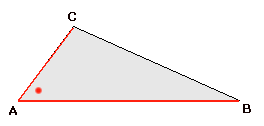
$
O\left( {\Delta ABC} \right) = \frac{1}
{2} \cdot AB \cdot AC \cdot \sin \angle A
$
In een regelmatige veelhoek zijn alle zijden even lang en alle hoeken even groot.
Voorbeeld
De oppervlakte van een regelmatige negenhoek is 180. Bereken in twee decimalen nauwkeurig de omtrek van de negenhoek.
Opmerking
Het rekenen met goniometrische verhoudingen met een verhoudingstabel is niet zo handig. Dat kan gemakkelijker.
- Zie berekeningen in driehoeken (wiskunde B)
De zijde × hoogte-methode
Voor driehoeken geldt:
- ene zijde × bijbehorende hoogte = andere zijde × de bijbehorende hoogte
Je kunt daarmee soms handig de onbekende lengtes in een driehoek uitrekenen.
Opgave 2
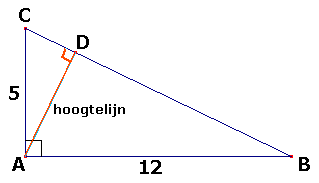
Gegeven is een rechthoekige $\Delta ABC$ met $\angle A=90^\circ$, $AB=12$ en $AC=5$. $AD$ is de hoogtelijn door het punt $A$.
- Bereken exact de lengte van AD.
- bewijs formule oppervlakte driehoek
- de regelmatige negenhoek uitgewerkt
- hint bij opgave 3
- opgave 1 en 2 uitgewerkt
- oppervlakte basisfiguren
- weekpuzzel 18 van 2018